Extra Questions: Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Chapter 2 Polynomials :

Question 1. Which of the following expressions are polynomials?

(i) x⁵ - 2x³ + + x + 7

Solution :

We have x⁵ - 2x³ + + x + 7

The highest degree of the variable = 5

(ii) \(\displaystyle \frac{1}{{\sqrt{2}}}{{x}^{2}}\,-\,\sqrt{2}x\,+\,2\)

Solution :

We have \(\displaystyle \frac{1}{{\sqrt{2}}}{{x}^{2}}\,-\,\sqrt{2}x\,+\,2\)

The highest degree of the variable = 2

Question 2. Coefficient of x in √3 - 2√2x + 4x²

Solution :

We have √3 - 2√2x + 4x²

The coefficient of x is 2√2x

Question 3. Classify the following as linear, quadratic, and cubic polynomials:

(i) 2x² + 4x

Solution :

We have 2x² + 4x

It is a quadratic polynomial.

Question 4. If p(x) = 5 - 4x + 2x² , find (i) p(0) (ii) p(3) (iii) p(-2)

Solution :

Given 5 - 4x + 2x²

[ After put x = 0 ]

5 - 4(0) + 2(0)²

= 5 - 0 + 2 × 0

= 5 - 0 + 0

= 5

[ After put x = 3 ]

5 - 4(3) + 2(3)²

= 5 - 12 + 2 × 9

= 5 - 12 + 18

= 23 - 12

= 11

[ After put x = -2 ]

5 - 4(-2) + 2(-2)²

= 5 + 8 + 2 × 4

= 5 + 8 + 8

= 21

After put p(0), p(3) and p(-2) we get 5, 11 and 21.

Question 5. Find the zero of the polynomial:

(i) p(x) = x - 5

Solution :

Given x - 5

x - 5 = 0

= x = 5

(ii) g(x) = 5 - 4x

Given 5 - 4x

5 - 4x = 0

= - 4x = - 5

= x = \(\displaystyle \frac{{-\,5}}{{-\,4}}\)

= x =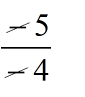

= x = \(\displaystyle \frac{{\,5}}{4}\)

Question 6. Using remainder theorem, find the remainder when.

(i) ( x³ - 6x² + 9x + 3 ) is divided by ( x - 1 )

Solution :

Let p(x) = x³ - 6x² + 9x + 3

So, x - 1 = 0

x = 1

Using remainder theorem,

when p(x) = x³ - 6x² + 9x + 3

than p ( 1 ) = ( 1 )³ - 6( 1 )² + 9 × 1 + 3

= 1 - 6 × 1 + 9 + 3

= 1 - 6 + 9 + 3

= 13 - 6

= 7

So, answer = 7

Question 7. Using factor theorem, show that:

(i) ( x - 2 ) is a factor of ( x³ - 8 )

Solution :

Let p(x) = x³ - 8

So, x - 2 = 0

x = 2

Using remainder theorem,

when p(x) = x³ - 8

than p ( 2 ) = ( 2 )³ - 8

= 8 - 8

= 0

So, p(x) is a factor of ( x³ - 8 )

Question 8. Find the value of k for which ( x - 1 ) is a factor of ( 2x³ + 9x² + x + k )

Solution :

Let p(x) = 2x³ + 9x² + x + k

Given x - 1 is factor of p(x)

So, x - 1 = 0

x = 1

Using the factor theorem,

when p( x ) = 2x³ + 9x² + x + k

than p(1) = 2(1)³ + 9(1)² + 1 + k

= 2 × 1 + 9 × 1 + 1 + k = 0

= 2 + 9 + 1 + k = 0

= 12k = 0

= k = -12

The value of k = -12

Question 9. Factorize :

(i) 18x²y - 24xyz

Solution :

Given 18x²y - 24xyz

18x²y - 24xyz [ find the common ]

= 6xy ( 3x - 4z )

So, answer = 6xy ( 3x - 4z )

(ii) x³ - 2x²y + 3xy² - 6y³

Solution :

Given x³ - 2x²y + 3xy² - 6y³

x³ - 2x²y + 3xy² - 6y³ [ find the common ]

= x² ( x - 2y ) + 3y² ( x - 2y )

= ( x² + 3y² ) ( x - 2y )

So, answer = ( x² + 3y² ) ( x - 2y )

Question 10. Factorize :

(i) 25x² - 64y²

Solution :

Given 25x² - 64y²

[ Using identity = ( a + b ) ( a - b ) = a² - b² ]

25x² - 64y²

= ( 5x + 8y ) ( 5x - 8y )

∴ 25x² - 64y² = ( 5x + 8y ) ( 5x - 8y )

(ii) ( 4x - 2y )³

Solution :

We have ( 4x - 2y )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 4x - 2y )³

= ( 4x )³ - ( 2y )³ - 3 × 4x × 2y ( 4x - 2y )

= 64x³ - 8y³ - 24xy ( 4x - 2y )

= 64x³ - 8y³ - 96x²y + 48xy²

So, answer = 64x³ - 8y³ - 96x²y + 48xy²

Question 11. Factorize :

(i) x² + 18x + 32

Solution :

Given x² + 18x + 32

[ Using the splitting the middle term method ]

So, x² + 18x + 32

= x² + 16x + 2x + 32 [ find the common ]

= x ( x + 16 ) + 2 ( x + 16 )

= ( x + 2 ) ( x + 16 )

(ii) 7x + 49x + 84

Solution :

Given 7x + 49x + 84

[ Using the splitting the middle term method ]

So, 7x + 49x + 84

= 7x + 28x + 21x + 84

= 7x ( 1 + 4 ) + 1x ( 1 + 4 )

= ( 7x + x ) ( 1 + 4 )

(iii) √2x² + 3x + √2

Solution :

Given √2x² + 3x + √2

[ Using the splitting the middle term method ]

√2x² + 2x + x + √2

= √2x ( x + √2 ) + 1 ( x + √2 )

= ( x + √2 ) ( √2x + 1 )

Question 12. Expand :

(i) ( a + 2b + 5c )²

Solution :

We have ( a + 2b + 5c )²

[ using identity = ( x + y + z )² = ( x² + y² + z² + 2xy + 2yz + 2zx ) ]

( a + 2b + 5c )²

= ( a )² + ( 2b )² + ( 5c )² + 2 × a × 2b + 2 × 2b × 5c + 2 × 5c × a

= a² + 4b² + 25c² + 4ab + 20bc + 10ac

So, answer = a² + 4b² + 25c² + 4ab + 20bc + 10ac

(ii) ( a - 2b - 3c )²

Solution :

We have ( a - 2b - 3c )²

[ using identity = ( x + y + z )² = ( x² + y² + z² + 2xy + 2yz + 2zx ) ]

( a - 2b - 3c )²

= ( a )² + ( -2b )² + ( -3c )² + 2 × a × ( -2b ) + 2 × ( -2b ) × ( -3c ) + 2 × ( -3c ) × a

= a² + 4b² + 9c² - 4ab + 12bc - 6ac

So, answer = a² + 4b² + 9c² - 4ab + 12bc - 6ac

Question 13. Factorize :

(i) 9x² + 16y² + 4z² - 24xy + 16yz - 12xz

Solution :

We have 9x² + 16y² + 4z² - 24xy + 16yz - 12xz

[ using identity = ( x + y + z )² = ( x² + y² + z² + 2xy + 2yz + 2zx ) ]

9x² + 16y² + 4z² - 24xy + 16yz - 12xz

= ( -3x)² + ( 4y )² + ( 2z )² + 2 × ( -3x ) × 4y + 2 × 4y × 2z + 2 × 2z × ( -3x )

= ( -3x + 4y + 2z )²

= ( -3x + 4y + 2z ) ( -3x + 4y + 2z )

So, answer = ( -3x + 4y + 2z ) ( -3x + 4y + 2z )

(ii) 4x² + 9y² + 16z² + 12xy - 24yz - 16xz

Solution :

We have 4x² + 9y² + 16z² + 12xy - 24yz - 16xz

[ using identity = ( x + y + z )² = ( x² + y² + z² + 2xy + 2yz + 2zx ) ]

4x² + 9y² + 16z² + 12xy - 24yz - 16xz

= ( 2x )² + ( 3y )² + ( -4z )² + 2 × 2x × 3y + 2 × 3y × ( -4z ) + 2 × ( -4z ) × 2x

= ( 2x + 3y - 4z )²

= ( 2x + 3y - 4z ) ( 2x + 3y - 4z )

So, answer = ( 2x + 3y - 4z ) ( 2x + 3y - 4z )

Question 14. Evaluate :

(i) ( 99 )²

Solution :

We have ( 99 )²

( 100 - 1 )²

[ using identity = ( x - y )² = x² - 2xy + y² ]

( 100 - 1 )²

= ( 100 )² - 2 × 100 × 1 + ( 1 )²

= 10000 - 200 + 1

= 10001 - 200

= 9801

So, answer = 9801

(ii) 991 × 1009

Solution :

We have 991 × 1009

( 1000 - 9 ) × ( 1000 + 9 )

[ using identity = x² - y² = ( x + y ) ( x - y) ]

( 1000 - 9 ) × ( 1000 + 9 )

= ( 1000 )² - ( 9 )²

= 1000000 - 81

= 999919

So, answer = 999919

(iii) 117 × 83

Solution :

We have 117 × 83

( 100 + 17 ) × ( 100 - 17 )

[ using identity = x² - y² = ( x + y ) ( x - y) ]

( 100 + 17 ) × ( 100 - 17 )

= ( 100 )² - ( 17 )²

= 10000 - 289

= 9711

So, answer = 9711

Question 15. Expand :

(i) ( \(\displaystyle \frac{2}{3}x\) + 1 )³

Solution :

We have ( \(\displaystyle \frac{2}{3}x\) + 1 )³

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) ]

( \(\displaystyle \frac{2}{3}x\) + 1 )³

= \(\displaystyle {{\left( {\frac{2}{3}x} \right)}^{3}}\) + ( 1 )³ + 3 × \(\displaystyle \left( {\frac{2}{3}x} \right)\) × 1 ( \(\displaystyle \left( {\frac{2}{3}x} \right)\) + 1 )

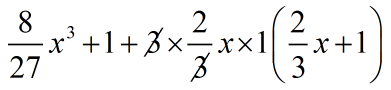
= \(\displaystyle \frac{8}{{27}}{{x}^{3}}\,+\,1+\,2x\,\times \,\left( {\frac{2}{3}x\,+\,1} \right)\)

= \(\displaystyle \frac{8}{{27}}{{x}^{3}}\,+\,1+\,\frac{4}{3}{{x}^{2}}\,+\,2x\)

So, answer = \(\displaystyle \frac{8}{{27}}{{x}^{3}}\,+\,1+\,\frac{4}{3}{{x}^{2}}\,+\,2x\)

(ii) ( 3a - 2b )³

Solution :

We have ( 3a - 2b )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 3a - 2b )³

= ( 3a )³ - ( 2b )³ - 3 × 3a × 2b ( 3a - 2b )

= 27a³ - 8b³ - 18ab ( 3a - 2b )

= 27a³ - 8b³ - 54a²b + 36ab²

So, answer = 27a³ - 8b³ - 54a²b + 36ab²

Question 16. Evaluate :

(i) ( 95 )³

Solution :

We have ( 95 )³

( 100 - 5 )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 100 - 5 )³

= ( 100 )³ - ( 5 )³ - 3 × 100 × 5 ( 100 - 5 )

= 1000000 - 125 - 1500 ( 100 - 5 )

= 1000000 - 125 - 150000 + 7500

= 1007500 - 150125

= 857375

So, answer = 857375

(ii) ( 0.2 )³ - ( 0. 3 )³ + ( 0.1 )³

Solution :

We have ( 0.2 )³ - ( 0. 3 )³ + ( 0.1 )³

= 0.008 - 0.0027 + 0.001

= 0.009 - 0.027

= 0.018

So, answer = 0.018

Question 17. Factorize :

(i) 125a³ + b³ + 64c³ - 60abc

Solution :

We have 125a³ + b³ + 64c³ - 60abc

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

125a³ + b³ + 64c³ - 60abc

= ( 5a + b + 4c ) ( 5a² + b² + 4c² - 5a × b + b × -4c - 4c × 5a )

= ( 5a + b + 4c ) ( 25a² + b² - 5ab - 4bc - 20ca )

So, answer = ( 5a + b + 4c ) ( 25a² + b² - 5ab - 4bc - 20ca )

(ii) 216 + 27b³ + 8c³ - 108bc

We have 216 + 27b³ + 8c³ - 108bc

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

216 + 27b³ + 8c³ - 108bc

= ( 6 + 3b + 2c ) ( 6² + 3b2 + 2c² - 6 × 3b - 3b × 2c - 2c × 6 )

= ( 6 + 3b + 2c ) ( 36 + 9b² + 4c² - 18b - 6bc - 12c )

So, answer = ( 6 + 3b + 2c ) ( 36 + 9b² + 4c² - 18b - 6bc - 12c )

Question 18. Find the product :

(i) ( x - 2y + 3 ) ( x2 + 4y2 + 2xy - 3x + 6y + 9 )

We have ( x - 2y + 3 ) ( x2 + 4y2 + 2xy - 3x + 6y + 9 )

Let, First bracket = ( x - 2y + 3 )

Second bracket = ( x2 + 4y2 + 2xy - 3x + 6y + 9 )

[ we have multiply to the first bracket by the second bracket ]

( x - 2y + 3 ) ( x2 + 4y2 + 2xy - 3x + 6y + 9 )

= x ( x2 + 4y2 + 2xy - 3x + 6y + 9 ) - 2y ( x2 + 4y2 + 2xy - 3x + 6y + 9 ) + 3 ( x2 + 4y2 + 2xy - 3x + 6y + 9 )

= x3 + 4xy2 + 2x2y - 3x2 + 6xy + 9x - 2x2y - 8y3 - 4xy2 + 6xy - 12y2 - 18y + 3x2 + 12y2 + 6xy - 9x + 18y + 27

= x3 + 6xy + 6xy + 6xy - 8y3 + 27

= x3 + 18xy - 8y3 + 27

= x3 - 8y3 + 27 + 18xy

So, answer = x3 - 8y3 + 27 + 18xy

Question 19. Write the following in the expanded form :

(i) ( 2a - 3b - c )2

Solution :

We have ( 2a - 3b - c )2

[ using identity = ( x + y + z )² = ( x² + y² + z² + 2xy + 2yz + 2zx ) ]

( 2a - 3b - c )2

= ( 2a )² + ( -3b )² + ( c )² + 2 × 2a × ( -3b ) + 2 × ( -3b ) × ( -c ) + 2 × ( -c ) × 2a

= 4a² + 9b² + c² - 12ab + 6bc - 4ca

So, answer = 4a² + 9b² + c² - 12ab + 6bc - 4ca

Question 20. Simplify each of the following :

(i) ( 4x + 2y )3 + ( 4x - 2y )3

Solution :

We have ( 4x + 2y )3 + ( 4x - 2y )3

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) and ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 4x + 2y )3 + ( 4x - 2y )3

= [ { ( 4x )3 + ( 2y )3 + 3 × 4x × 2y ( 4x + 2y ) } + { ( 4x )3 - ( 2y )3 - 3 × 4x × 2y ( 4x - 2y ) } ]

= 64x3 + 8y3 + 24xy ( 4x + 2y ) + 64x3 - 8y3 - 24xy ( 4x - 2y )

= 64x3 + 8y3 + 96x2y + 48xy2 + 64x3 - 8y3 - 96x2y + 48xy2

= 64x3 + 64x3+ 48xy2 + 48xy2

= 128x3 + 96xy2

So, answer = 128x3 + 96xy2

(ii) 175 × 175 + 2 × 174 × 25 + 25 × 25

Solution :

Given 175 × 175 + 2 × 175 × 25 + 25 × 25

Multiply all these

= 30625 + 8750 + 625

= 40000

S0, answer = 40000 .

NCERT Class 9 Maths Chapter 2 Polynomials :

Extra Questions Class 9 Maths Chapter 2 Polynomials

Extra Questions: Class 9 Maths Chapter 2 Polynomials

Leave a Comment Cancel Reply