NCERT Solutions Class 8 Maths Chapter 1 Rational Numbers
NCERT Class 8 Maths Chapter 1 Rational Numbers :
Class 8 Maths Exercise 1.1 (Page-14)
Q1. Using appropriate properties find.

(ii) \(\displaystyle \frac{2}{5}\times \left( {\frac{{-3}}{7}} \right)-\frac{1}{6}\times \frac{3}{2}+\frac{1}{{14}}\times \frac{2}{5}\)
Solution :
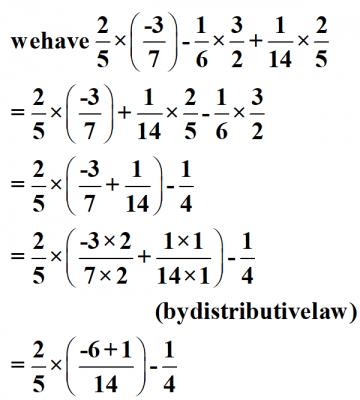
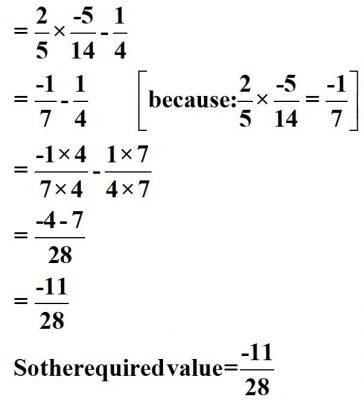
Q2. Write the additive inverse of each of the following.
(i) \(\displaystyle \frac{2}{8}\)
Solution :
\(\displaystyle Additive\text{ }inverse\text{ }of\frac{2}{8}=-\left( {\frac{2}{8}} \right)=\frac{{-2}}{8}\)
(ii) \(\displaystyle \frac{{-5}}{9}\)
Solution :
\(\displaystyle Additive\text{ }inverse\text{ }of\frac{{-5}}{9}=-\left( {\frac{{-5}}{9}} \right)=\frac{5}{9}\)
(iii) \(\displaystyle \frac{{-6}}{-5}\)
Solution :
\(\displaystyle Additive\text{ }inverse\text{ }of\frac{{-6}}{{-5}}=-\left( {\frac{{-6}}{{-5}}} \right)=\frac{{-6}}{5}\)
(iv) \(\displaystyle \frac{{2}}{-9}\)
Solution :
\(\displaystyle Additive\text{ }inverse\text{ }of\frac{2}{{-9}}=-\left( {\frac{2}{{-9}}} \right)=\frac{2}{9}\)
(v) \(\displaystyle \frac{{19}}{-6}\)
Solution :
\(\displaystyle Additive\text{ }inverse\text{ }of\frac{{19}}{{-6}}=\frac{{-19}}{6}=-\left( {\frac{{-19}}{6}} \right)=\frac{{19}}{6}\)
Q3. Verify that -(-x)=x for.
(i) \(\displaystyle x=\frac{{11}}{{15}}\)
Solution :
\(\displaystyle \begin{array}{l}We\,have\,x=\frac{{11}}{{15}}\\so\,\,\,\,\,\,\,\,-x=\frac{{-11}}{{15}}\\\,\,\,\,\,\,\,\,\,\,\,-\left( {-x} \right)=-\left( {\frac{{-11}}{{15}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{{11}}{{15}}\,\,(verified)\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {because\,:\,\,(-)\times (-)=(+)} \right]\end{array}\)
(ii) \(\displaystyle x=\frac{{-13}}{{17}}\)
Solution :
\(\displaystyle \begin{array}{l}We\,have\,x=\frac{{-13}}{{17}}\\so\,\,\,\,\,\,\,\,-x=-\left( {\frac{{-13}}{{17}}} \right)=\frac{{13}}{{17}}\\\,\,\,\,\,\,\,\,\,\,\,-\left( {-x} \right)=-\left( {\frac{{13}}{{15}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{{-13}}{{17}}\,\,(verified)\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {because\,:\,\,(-)\times (-)=(+)} \right]\end{array}\)
Q4. Find the multiplicative inverse of the following.
(i) -13
Solution :
\(\displaystyle \begin{array}{l}We\,know\,that\,multiplicative\,inverse\,of\,a=\frac{1}{a}\\So,\,-13=\frac{{-1}}{{13}}\,\,\,\,\,\,\,\,\,\left[ {because\,-13\times \frac{{-1}}{{13}}\,=1} \right]\end{array}\)
(ii) \(\displaystyle \frac{{-13}}{19}\)
Solution :
\(\displaystyle \begin{array}{l}We\,know\,that\,multiplicative\,inverse\,of\,a=\frac{1}{a}\\So,\,\frac{{-13}}{{19}}=\frac{{-19}}{{13}}\,\,\,\,\,\,\,\,\,\left[ {because\,\frac{{-13}}{{19}}\times \frac{{-19}}{{13}}\,\,\,\,=1} \right]\end{array}\)
(iii) \(\displaystyle \frac{{1}}{5}\)
Solution :

(iv) \(\displaystyle \frac{{-5}}{8}\times \frac{{-3}}{7}\)
Solution :
\(\displaystyle \begin{array}{l}Multiplicative\,inverse\,of\\\frac{{-5}}{8}\times \frac{{-3}}{7}=\frac{{-8}}{5}\times \frac{{-7}}{3}=\frac{{56}}{{15}}\\=Alternatively:\frac{{-5}}{8}\times \frac{{-3}}{7}=\frac{{15}}{{56}}\\so,\,Multiplicative\,inverse\,of\,\\\frac{{15}}{{56}}=\frac{{56}}{{15}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {Because\frac{{15}}{{56}}\times \frac{{56}}{{15}}=1} \right]\end{array}\)
(v) \(\displaystyle -1\times \frac{{-2}}{5}\)
Solution :
\(\displaystyle \begin{array}{l}multiplicative\,inverse\,of\,-1\times \frac{{-2}}{5}=\frac{2}{5}=\frac{5}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {because\,:\,\frac{2}{5}\times \frac{5}{2}=1} \right]\,\end{array}\)
(vi) \(\displaystyle -1\)
Solution :
\(\displaystyle \begin{array}{l}multiplicative\,inverse\,of\,-1=\frac{1}{{-1}}=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {because:\,\,\,-1\times \frac{1}{{-1}}=1} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Q5. Name the property under multiplication used in each of the following.
(i) \(\displaystyle \,\frac{{-4}}{5}\times 1=1\times \frac{{-4}}{5}=\frac{{-4}}{5}\)
Solution :
We know very well : 1 is the multiplicative identity
(ii) \(\displaystyle \,\frac{{-13}}{{17}}\times \frac{{-2}}{7}=\frac{{-2}}{7}\times \frac{{-13}}{{17}}\)
Solution :
We know that it's "Commutativity"
(iii) \(\displaystyle \frac{{-19}}{{29}}\times \frac{{29}}{{-19}}=1\)
Solution :
We know that it's "Multiplicative inverse"
NCERT Solutions Class 8 Maths Chapter 1 Rational Numbers
Exercise 1.1 (Page-14)
Q6. \(\displaystyle Multiply\,\frac{6}{{13}}\,by\,the\,reciprocal\,of\,\frac{{-7}}{{16}}.\)
Solution :
\(\displaystyle \begin{array}{l}Reciprocal\,of\,\frac{{-7}}{{16}}=\frac{{-16}}{7}\\So,\,\frac{6}{{13}}\times \frac{{-16}}{7}=\frac{{6\times (-16)}}{{13\times 7}}=\frac{{-96}}{{91}}\end{array}\)
Q7. Tell what property allows you to compute
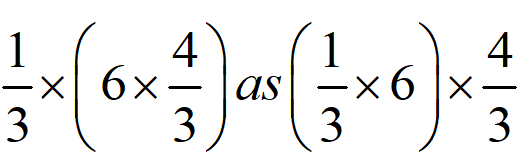
Solution :
\(\displaystyle \begin{array}{l}we\,know\,that\,(a\times b)\times c=a\times (b\times c)\\so,\,\,\frac{1}{3}\times \left( {6\times \frac{4}{3}} \right)\,=\,\left( {\frac{1}{3}\times 6} \right)\times \frac{4}{3}\\it's\,shows\,the\,property\,of\,multiplication.\end{array}\)
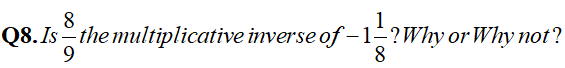
Solution :
\(\displaystyle \begin{array}{l}We\,have\,-1\frac{1}{8}=\frac{{-9}}{8}\\because\,multiplicative\,inverse\,of\,\frac{8}{9}\,is\,\frac{9}{8}\,but\,not\,\frac{{-9}}{8}\\So,\,\frac{8}{9}\,is\,not\,the\,multiplicative\,inverse\,of\,-1\frac{1}{8}\end{array}\)
Q9. \(\displaystyle Is\,0.3\,the\,multiplicative\,inverse\,of\,3\frac{1}{3}?\,Why\,or\,why\,not?\)
Solution :
\(\displaystyle \begin{array}{l}We\,have\,3\frac{1}{3}=\frac{{10}}{3}\,and\,0.3=\frac{3}{{10}}\\also\,\frac{{10}}{3}\times \frac{3}{{10}}=1\\multiplicative\,inverse\,of\,0.3\,or\,\frac{3}{{10}}=\frac{{10}}{3}\\so,\,0.3\,is\,the\,multiplicative\,inverse\,of\,3\frac{1}{3}\end{array}\)
NCERT Solutions Class 8 Maths Chapter 1 Rational Numbers
Exercise 1.1 (Page-15)
Q10. Write.
(i) The rational number that does not have a reciprocal.
Solution :
\(\displaystyle \begin{array}{l}0\,\,is\,the\,rational\,number\,which\,does\,not\,have\,its\,reciprocal\,\\\left[ {therefore\,\frac{1}{0}is\,not\,defined} \right]\end{array}\)
(ii) The rational number that are equal to their reciprocals.
Solution :
\(\displaystyle \begin{array}{l}Reciprocal\,of\,1=\frac{1}{1}=1\\Reciprocal\,of\,-1=\frac{1}{{-1}}=-1\\So,\,1\,and\,-1\,are\,the\,required\,rational\,number.\end{array}\)
(iii) The rational number that is equal to its negative.
Solution :
\(\displaystyle 0\,is\,the\,rational\,number\,which\,is\,equal\,to\,its\,negative.\)
Q11. Fill in the blanks.
(i) Zero has ____________ reciprocal.
(ii) The numbers__________ and ___________ are their own reciprocals.
(iii) The reciprocal of -5 is_________.
(iv) reciprocal of \(\displaystyle \frac{1}{x}\), where \(\displaystyle x\) \(\displaystyle \ne \) 0 is________.
(v) The product of two rational numbers is always a______________.
(vi) The reciprocal of a positive rational number is_______________.
Solution :
(i) No.
(ii) 1,-1.
(iii) \(\displaystyle \frac{{-1}}{5}\).
(iv) \(\displaystyle x\)
(v) Rational number.
(vi) Positive.
