NCERT Solutions Class 9 Maths Chapter 5 Introduction to Euclid's Geometry Exercise 5.1
Introduction :
In this exercise we will learn about Introduction to Euclid's Geometry. Euclid's definitions, Axioms and postulates. You know its boundaries are called surfaces. The boundaries of the surface are curves or straight lines. These lines end in points.
7 of Euclid's axioms, are given below.
- Things which are equal to the same things are equal to one another.
- If equals are added to equals, the wholes are equal.
- If equals are subtract from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
- Things which are double of the same things are equal to one another.
- Things which are halves of the same things are equal to one another.
5 of postulate are given below.
- A straight line may be drawn from any one point to any other point.
- A terminated line can be produced indefinitely.
- A circle can be drawn with any center and any radius.
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry :
- NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry Exercise 5.1
- NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry Exercise 5.2
Class 9 Maths Exercise 5.1 (Page-85)
Q1. Which of the following statements are true and which are false? Give reason for your answers.
(i) Only one line can pass through a single point.
Solution :
False, because infinite line can pass through a single point.

(ii) There are an infinite number of lines which pass through two distinct points.
Solution :
False, because only one line can pass through two distinct points.

(iii) A terminated line can be produced indefinitely on both the sides.
Solution :
True, because a terminated line can be produced infinite on both the sides.

(iv) If two circle are equal, then the radii are equal.
Solution :
True, because both circle are equal, then radii are equal. see figure

(v) In figure, if AB = PQ and PQ = XY, then XY = AB .
Solution :
True, XY = AB because all three lines are equal . The first axiom of Euclid.
Q2. Give a definition for each of the following terms. Are there other terms that need to be defined firest? What are they, and how might you define them?
(i) parallel lines
Solution :
Parallel lines are always equal because having no common point, are parallel lines.
(ii) perpendicular lines
Solution :
Perpendicular lines have two lines make \(\displaystyle {{90}^{\circ }}\) angle.
(iii) lines segment
Solution :
Line segment which have two end point and will make \(\displaystyle {{180}^{\circ }}\) angle.
(iv) radius of a circle
Solution :
The line segment with one end point at the center and the other at any point on the circle.
(v) square
Solution :
In square all four sides are equal and all four sides are make \(\displaystyle {{90}^{\circ }}\)/ right angles.
Q3. Consider two ' postulate ' given below:
(i) Given any two distinct point A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these ' postulates ' contain any undefined terms? Are these postulate consistent?
Do they follow from Euclid's postulate? Explain .
Solution :
Yes, these postulate many undefined terms. Yes, they are consistent because they refer to two different situations.
No, these postulate do not follow Euclid's postulates. They follow on axiom ' Given two distinct points there is a unique line that pass through them.
NCERT Solutions Class 9 Maths Chapter 5 Introduction to Euclid's Geometry Exercise 5.1
Q4. If a point C lies between two points A and B such that AC = BC, then prove that AC = \(\displaystyle \frac{1}{2}\)AB . Explain by drawing the figure.
Solution :
We have
![]()
Given : AC = BC
To prove : AC = \(\displaystyle \frac{1}{2}\)AB
Proof : AC = BC [ given ]
adding both sides by AC
AC + AC = BC + AC [ equals are added to equals ]
2AC = AB [ AC + BC coincide AB ]
AC = \(\displaystyle \frac{1}{2}\)AB
[ Hence proved ].
Q5. In Question 4, point C is called a mid -point of line segment AB. Prove that every line segment has one and only one mid-point.
Solution :

Let C and D two mid-point of a AB.
AC = \(\displaystyle \frac{1}{2}\)AB (i)
AD = \(\displaystyle \frac{1}{2}\)AB (ii)
Subtract (i) from (ii)
AC - AD = \(\displaystyle \frac{1}{2}\)AB - \(\displaystyle \frac{1}{2}\)AB
AC - AD = 0
AC = AD [ It means C and D coincide ]
∴ Every line segment has one and only one mid point.
Q6. In fig. 5.10, if AB = BD, then prove that AB = CD.
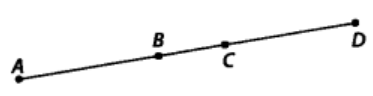
Solution :
Given : AC = BD
To prove : AB = CD
Proof : AC = BD [ given ]
subtract both sides by BC
AB - BC = CD - BC
AB = CD - BC + BC [ because - BC + BC = 0 ]
AB = CD
[ Hence proved ]
Q7. Why is Axiom 5, in the list of Euclid's axioms, considered a ' universal truth '? ( Note that the question is not about the fifth postulate. )
Solution :
Axiom 5 = The whole is greater than the part.
∴ Yes, this statement is universal truth in the world.
NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry :