NCERT Solutions Class 9 Maths Chapter 2 Polynomials Exercise 2.2
Introduction:
In this exercise/article we will learn about Polynomials. Zeroes of the polynomial. A zero of a polynomial need to not be 0. 0 may be a zero of a polynomial. Every linear polynomial has one and only one zero. A polynomial can have more than one zero.
NCERT Class 9 Maths Chapter 2 Polynomials :
- NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.1
- NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.2
- NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.3
- NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.4
- NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.5
- Extra Questions Class 9 Maths Chapter 2 Polynomials
Class 9 Maths Exercise 2.2 (Page-34)
Q1. Find the value of the polynomial 5x - 4x2 + 3 at
(i) x = 0
Solution :
Given 5x - 4x2 + 3
Now, 5 × 0 - 4 ( 0 )2 + 3 [ put x = 0 ]
= 0 - 4 × 0 + 3
= 0 - 0 + 3 [ because 0 - 0 = 0 ]
= 3
So, answer is 3
(ii) x = -1
Solution :
Given 5x - 4x2 + 3
Now, 5 ( -1 ) - 4 (-1 )2 + 3 [ put x = -1 ]
= - 5 - 4 × 1 + 3
= - 5 - 4 + 3
= - 9 + 3
= - 6
So, answer is - 6
(iii) x = 2
Solution :
Given 5x - 4x2 + 3
Now, 5 × 2 - 4 ( 2 )2 + 3 [ put x = 2 ]
= 10 - 4 × 4 + 3
= 10 - 16 + 3
= 13 - 16
= - 3
So, answer is - 3
Q2. Find p(0), p(1) and p(2) for each of the following polynomials :
(i) p(y) = y2 - y + 1
Solution :
Given y2 - y + 1
[ After put y = 0 ]
( 0 )2 - 0 + 1
= 0 - 0 + 1 [ because 0 - 0 = 0 ]
= 1
[ After put y = 1 ]
( 1 )2 - 1 + 1
= 1 - + 1
= 1
[ After put y = 2 ]
( 2 )2 - 2 + 1
= 4 - 2 + 1
= 5 - 2
= 3
After put p(0), p(1) and p(2) we get 1, 1 and 3.
(ii) p(t) = 2 + t + 2t2 - t3
Solution :
Given 2 + t + 2t2 - t3
[ After put t = 0 ]
2 + 0 + 2 ( 0 )2 - ( 0 )3
= 2 + 0 + 2 × 0 - 0
= 2 + 0 + 0 - 0 [ because 0 - o = o ]
= 2
[ After put t = 1 ]
2 + 1 + 2 ( 1 )2 - ( 1 )3
2 + 1 + 2 × 1 - 1
= 2 + 1 + 2 - 1 [ because 1 - 1 = 0 ]
= 4
[ After put t = 2 ]
2 + 2 + 2 ( 2 )2 - ( 2 )3
2 + 2 + 2 × 4 - 8
= 2 + 2 + 8 - 8 [ because 8 - 8 = 0 ]
= 4
After put p(0), p(1) and p(2) we get 2, 4 and 4.
(iii) p( x ) = x3
Solution :
Given x3
[ After put x = 0 ]
( 0 )3
= 0
[ After put x = 1 ]
( 1 )3
= 1
[ After put x = 2 ]
( 2 )3
= 8
After put p(0), p(1) and p(2) we get 0, 1 and 8.
(iv) p(x) = ( x - 1 ) ( x + 1 )
Solution :
Given ( x - 1 ) ( x + 1 ) [ using identity = ( x - y ) ( x + y ) = x2 - y2 ]
[ After put x = 0 ]
= ( 0 )2 - ( 1 )2
= 0 - 1
= -1
[ After put x = 1 ] [ using identity = ( x - y ) ( x + y ) = x2 - y2 ]
= ( 1 )2 - ( 1 )2
= 1 - 1
= 0
[ After put x = 2 ] [ using identity = ( x - y ) ( x + y ) = x2 - y2 ]
= ( 2 )2 - ( 1 )2
= 4 - 1
= 3
After put p(0), p(1) and p(2) we get -1, 0 and 3.
NCERT Solutions Class 9 Maths
Q3. Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x) = 3x + 1 , x = \(\displaystyle -\,\frac{1}{3}\)
Solution :
Given p(x) = 3x + 1 , x = \(\displaystyle -\,\frac{1}{3}\)
[ After put x = \(\displaystyle -\,\frac{1}{3}\) ]
3 \(\displaystyle \left( {-\,\frac{1}{3}} \right)\) + 1
= 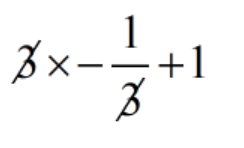
= - 1 + 1
= 0
So, \(\displaystyle -\,\frac{1}{3}\) is a zero of the polynomial 3x + 1 .
(ii) p(x) = 5x - \(\displaystyle \pi \) , x = \(\displaystyle \frac{4}{5}\)
Solution :
Given p(x) = 5x - \(\displaystyle \pi \) , x = \(\displaystyle \frac{4}{5}\)
[ After put x = \(\displaystyle \frac{4}{5}\) ]
5 × \(\displaystyle \frac{4}{5}\) + \(\displaystyle \pi \)
= 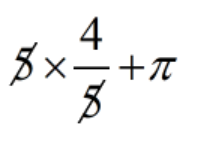
= 4 + \(\displaystyle \frac{4}{5}\)
So, \(\displaystyle \frac{4}{5}\) is a not zero of the polynomial 5x + 1 .
(iii) p(x) = x2 - 1 , x = 1 , -1
Solution :
Given p(x) = x2 - 1 , x = 1 , -1
[ After put x = 1 ]
( 1 )2 - 1
= 1 - 1
= 0
[ After put x = -1 ]
( - 1 )2 - 1
= 1 - 1
= 0
So, 1 and -1 is a zero of the polynomial x2 - 1 .
(iv) p(x) = ( x + 1 ) ( x - 2 ) , x = -1 , 2
Solution :
Given p(x) = ( x + 1 ) ( x - 2 ) , x = -1 , 2
[ After put x = -1 ]
( - 1 + 1 ) ( - 1 - 2 )
= ( 0 ) ( - 3 )
= 0 × - 3
= 0
[ After put x = 2 ]
( 2 + 1 ) ( 2 - 2 )
= ( 3 ) ( 0 )
= 3 × 0
= 0
So, -1 and 2 is a zero of the polynomial ( x + 1 ) ( x - 2 ) .
(v) p(x) = x2 , x = 0
Solution :
Given p(x) = x2 , x = 0
[ After put x = 0 ]
= ( 0 )2
= 0
So, 0 is a zero of the polynomial x2 .
(vi) p(x) = lx + m , x = \(\displaystyle -\,\frac{m}{l}\)
Solution :
Given p(x) = lx + m , x = \(\displaystyle -\,\frac{m}{l}\)
[ After put x = \(\displaystyle -\,\frac{m}{l}\) ]
l \(\displaystyle \left( {-\,\frac{m}{l}} \right)\) + m
= 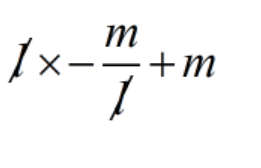
= - m + m
= o
So, \(\displaystyle -\,\frac{m}{l}\) is a zero of the polynomial lx + m .
(vii) p(x) = 3x2 - 1 , x = \(\displaystyle -\,\frac{1}{{\sqrt{3}}}\,,\,\frac{2}{{\sqrt{3}}}\)
Solution :
Given p(x) = 3x2 - 1 , x = \(\displaystyle -\,\frac{1}{{\sqrt{3}}}\,,\,\frac{2}{{\sqrt{3}}}\)
[ After put x = \(\displaystyle {-\,\frac{1}{{\sqrt{3}}}}\) ]
3 \(\displaystyle {{\left( {-\,\frac{1}{{\sqrt{3}}}} \right)}^{2}}\) - 1
= 3 × \(\displaystyle \frac{1}{3}\) - 1
= 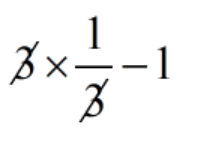
= 1 - 1
= 0
[ After put x = \(\displaystyle \frac{2}{{\sqrt{3}}}\) ]
3 \(\displaystyle {{\left( {\frac{2}{{\sqrt{3}}}} \right)}^{2}}\) - 1
= 3 × \(\displaystyle \left( {\frac{4}{3}} \right)\) - 1
= 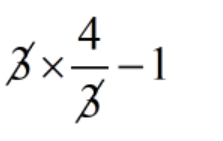
= 4 - 1
= 3
So, \(\displaystyle -\frac{1}{{\sqrt{3}}}\) is a zero but \(\displaystyle \frac{2}{{\sqrt{3}}}\) is not a zero of the polynomial 3x2 - 1 .
(viii) p(x) = 2x + 1 , x = \(\displaystyle \frac{1}{2}\)
Solution :
Given p(x) = 2x + 1 , x = \(\displaystyle \frac{1}{2}\)
[ After put x = \(\displaystyle \frac{1}{2}\) ]
2 \(\displaystyle \left( {\frac{1}{2}} \right)\) + 1
= \(\displaystyle 2\,\times \,\frac{1}{2}\,+\,1\)
= 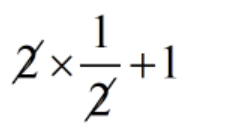
= 1 + 1
= 2
So, \(\displaystyle \frac{1}{2}\,\) is not a zero of the polynomial 2x + 1 .
Q4. Find the zero of the polynomial in each of the following cases :
(i) p(x) = x + 5
Solution :
Given p(x) = x + 5
[ After put x = 0 ]
x + 5 = 0
x = - 5
So, - 5 is zero of the polynomial x .
(ii) p(x) = x - 5
Solution :
Given p(x) = x - 5
[ After put x = 0 ]
x - 5 = 0
x = 5
So, 5 is zero of the polynomial x .
(iii) p(x) = 2x + 5
Solution :
Given p(x) = 2x + 5
2x + 5 = 0
2x = - 5
x = \(\displaystyle -\,\frac{5}{2}\)
So, \(\displaystyle -\,\frac{5}{2}\) is zero of the polynomial x .
(iv) p(x) = 3x - 2
Solution :
Given p(x) = 3x - 2
3x - 2 = 0
3x = 2
x = \(\displaystyle \frac{2}{3}\)
So, \(\displaystyle \frac{2}{3}\) is zero of the polynomial x .
(v) p(x) = 3x
Solution :
Given p(x) = 3x
3x = 0
x = - 3
So, - 3 is zero of the polynomial x .
(vi) p(x) = ax, a \(\displaystyle \ne \) 0
Solution :
Given p(x) = ax, a \(\displaystyle \ne \) 0
ax = 0
x = \(\displaystyle \frac{0}{a}\)
x = 0
So, 0 is zero of the polynomial x .
(vii) p(x) = cx + d, c \(\displaystyle \ne \) 0 , c , d are real numbers.
Solution :
Given p(x) = cx + d, c \(\displaystyle \ne \) 0 , c , d are real numbers
cx + d = 0
cx = - d
x = \(\displaystyle -\,\frac{d}{c}\)
So, \(\displaystyle -\,\frac{d}{c}\) is zero of the polynomial x .