NCERT Solutions Class 9 Maths Chapter 2 Polynomials Exercise 2.5

 

Introduction:

In this exercise/article we will learn about Polynomials. Algebraic identities with Examples & Solutions.

• Identity I : ( x + y )² = x² + 2xy + y²
• Identity II : ( x - y )² = x² - 2xy + y²
• Identity III : x² - y² = ( x + y ) ( x - y)
• Identity IV : ( x + a ) ( x + b ) = x² + ( a + b ) x + ab
• Identity V : ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx )
• Identity VI : ( x + y )³ = x³ + y³ + 3xy ( x + y )
• Identity VII : ( x - y )³ = x³ - y³ - 3xy ( x - y )
• Identity VIII : x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) .

NCERT Class 9 Maths Chapter 2 Polynomials :

• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.1
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.2
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.3
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.4
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.5
• Extra Questions Class 9 Maths Chapter 2 Polynomials

Class 9 Maths Exercise 2.5 (Page-48)

Q1. Use suitable identities to find the following products :

(i) ( x + 4 ) ( x + 10 )

Solution :

Given ( x + 4 ) ( x + 10 )

[ Using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

( x )² + ( 4 + 10 ) × x + 4 × 10

= x² + ( 14 ) × x + 40

= x² + 14x + 40

So, answer = x² + 14x + 40

(ii) ( x + 8 ) ( x - 10 )

Solution :

Given ( x + 8 ) ( x - 10 )

[ Using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

( x )² + ( 8 - 10 ) × x + 8 × ( - 10 )

= x² - 2 × x - 80

= x² - 2x - 80

So, answer = x² - 2x - 80

(iii) ( 3x + 4 ) ( 3x - 5 )

Solution :

Given ( 3x + 4 ) ( 3x - 5 )

[ Using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

( 3x )² + ( 4 - 5 ) × 3x + 4 × ( - 5 )

= 9x² - ( 1 ) × 3x - 20

= 9x² - 3x - 20

So, answer is 9x² - 3x - 20

(iv) ( y² + \(\displaystyle \frac{3}{2}\) )

Solution :

Given ( y² + \(\displaystyle \frac{3}{2}\) )

[ Using identity = ( a + b ) ( a - b ) = a² - b² ]

\(\displaystyle {{(\,{{y}^{2}}\,)}^{2}}\,-\,{{(\,\frac{3}{2}\,)}^{2}}\)

= \(\displaystyle {{y}^{4}}\,-\,\frac{9}{4}\)

So, answer = \(\displaystyle {{y}^{4}}\,-\,\frac{9}{4}\)

(v) ( 3 - 2x ) ( 3 + 2x )

Solution :

Given ( 3 - 2x ) ( 3 + 2x )

[ Using identity = ( a + b ) ( a - b ) = a² - b² ]

( 3 )² - ( 2x )²

= 9 - 4x²

So, answer = 9 - 4x²

Q2. Evaluate the following products without multiplying directly :

(i) 103 × 107

Solution :

We have 103 × 107

( 100 + 3 ) × ( 100 + 7 )

[ Using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

( 100 )² + ( 3 + 7 ) 100 + 3 × 7

= 10000 + ( 10 ) × 100 + 21

= 10000 + 1000 + 21

= 11021

So, answer = 11021

(ii) 95 × 96

Solution :

We have 95 × 96

( 100 - 5 ) × ( 100 - 4 )

[ Using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

( 100 )² + ( - 5 - 4 ) 100 + ( - 5 ) × ( - 4 )

= 10000 + ( - 9 ) × 100 + 20

= 10000 - 900 + 20

= 10020 - 900

= 9120

So, answer = 9120

(iii) 104 × 96

Solution :

We have 104 × 96

( 100 + 4 ) × ( 100 - 4 )

[ Using identity = ( a + b ) ( a - b ) = a² - b² ]

( 100 )² - ( 4 )²

= 10000 - 16

= 9984

So, answer = 9984

Q3. Factorise the following using appropriate identities :

(i) 9x² + 6xy + y²

Solution :

We have 9x² + 6xy + y²

[ using identity = ( a + b )² = a² + 2ab + b² ]

( 3x )² + 2 × 3x × y + ( y )²

= ( 3x + y )²

= ( 3x + y ) ( 3x + y )

So, answer = ( 3x + y ) ( 3x + y )

(ii) 4y² - 4y + 1

Solution :

We have 4y² - 4y + 1

[ using identity = ( a - b )² = a² - 2ab + b² ]

( 2y )² - 2 × 2y × 1 + ( 1 )²

= ( 2y - 1 )²

= ( 2y - 1 ) ( 2y - 1 )

So, answer = ( 2y - 1 ) ( 2y - 1 )

(iii) x² - \(\displaystyle \frac{{{{y}^{2}}}}{{100}}\)

Solution :

We have x² - \(\displaystyle \frac{{{{y}^{2}}}}{{100}}\)

[ Using identity = ( a + b ) ( a - b ) = a² - b² ]

( x )² - ( \(\displaystyle \frac{y}{{10}}\) )²

( x + \(\displaystyle \frac{y}{{10}}\) ) ( x - \(\displaystyle \frac{y}{{10}}\) )

So, answer = ( x + \(\displaystyle \frac{y}{{10}}\) ) ( x - \(\displaystyle \frac{y}{{10}}\) )

Q4. Expand each of the following, using suitable identities :

(i) ( x + 2y + 4z )²

Solution :

We have ( x + 2y + 4z )²

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( x )² + ( 2y )² + ( 4z )² + 2 × x × 2y + 2 × 2y × 4z + 2 × x × 4z

= x² + 4y² + 16z² + 4xy + 16yz + 8xz

So, x² + 4y² + 16z² + 4xy + 16yz + 8xz

(ii) ( 2x - y + z )²

Solution :

We have ( 2x - y + z )²

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( 2x )² + ( - y )² + ( z )² + 2 × 2x × ( -y ) + 2 × ( -y ) × z + 2 × z × 2x

= 4x² + y² + z² - 4xy - 2yz + 4xz

So, answer = 4x² + y² + z² - 4xy - 2yz + 4xz

(iii) ( - 2x + 3y + 2z )²

Solution :

We have ( - 2x + 3y + 2z )²

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( - 2x )² + ( 3y )² + ( 2z )² + 2 × ( -2x ) × 3y + 2 × 3y × 2z + 2 × 2z × ( -2x )

= 4x² + 9y² + 4z² - 12xy + 12yz - 8xz

So, answer = 4x² + 9y² + 4z² - 12xy + 12yz - 8xz

(iv) ( 3a - 7b - c )²

Solution :

We have ( 3a - 7b - c )²

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( 3a )² + ( -7b )² + ( -c )² + 2 × 3a × ( -7b ) + 2 × ( -7b ) × ( -c ) + 2 × ( -c ) × 3a

= 9a²  + 49b² + c² - 42ab + 14bc - 6ac

So, answer = 9a²  + 49b² + c² - 42ab + 14bc - 6ac

(v) ( - 2x + 5y - 3z )²

Solution :

We have ( - 2x + 5y - 3z )²

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( -2x )² + ( 5y )² + ( -3z )² + 2 × ( -2x ) × 5y + 2 × 5y ×  ( -3z ) + 2 × ( -3z ) × ( -2x )

= 4x² + 25y² + 9z² - 20xy - 30yz + 12xz

So, answer = 4x² + 25y² + 9z² - 20xy - 30yz + 12xz

(v) \(\displaystyle {{\left[ {\frac{1}{4}a-\frac{1}{2}b+1} \right]}^{2}}\)

Solution :

We have \(\displaystyle {{\left[ {\frac{1}{4}a-\frac{1}{2}b+1} \right]}^{2}}\)

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

=

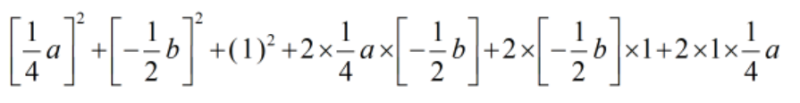
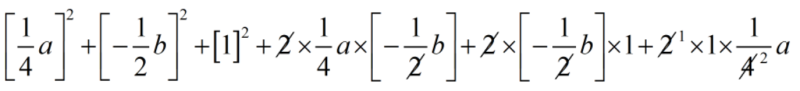
= \(\displaystyle \frac{a}{{16}}\,+\,\frac{b}{4}\,+\,1\,-\,\frac{{ab}}{4}\,-\,b\,+\,\frac{a}{2}\,\)

So, answer = \(\displaystyle \frac{a}{{16}}\,+\,\frac{b}{4}\,+\,1\,-\,\frac{{ab}}{4}\,-\,b\,+\,\frac{a}{2}\,\)

Q5. Factorise :

(i) 4x² + 9y² + 16z² + 12xy - 24yz - 16xz

Solution :

We have 4x² + 9y² + 16z² + 12xy - 24yz - 16xz

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( 2x )² + ( 3y )² + ( -4z )² + 2 × 2x × 3y + 2 × 3y × -4z + 2 × -4z × 2x

= ( 2x + 3y - 4z )²

= ( 2x + 3y - 4z ) ( 2x + 3y - 4z )

So, answer = ( 2x + 3y - 4z ) ( 2x + 3y - 4z )

(ii) 2x² + y² + 8z² - 2√2xy + 4√2yz - 8xz

Solution :

We have 2x² + y² + 8z² - 2√2xy + 4√2yz - 8xz

[ using identity = ( x + y + z )² = ( x² + y² + z²  + 2xy + 2yz + 2zx ) ]

( -√2x )² + ( y )² + ( 2√2z )² + 2 × ( -√2x ) × y + 2 × y × 2√2z + 2 × 2√2z × ( -√2x )

= ( -√2x + y + 2√2z )²

= ( -√2x + y + 2√2z ) ( -√2x + y + 2√2z )

So, answer = ( -√2x + y + 2√2z ) ( -√2x + y + 2√2z )

Q6. Write the following cubes in expanded form :

(i) ( 2x + 1 )³

Solution :

We have ( 2x + 1 )³

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) ]

( 2x )³ + ( 1 ) + 3 × 2x × 1 ( 2x + 1 )

= 8x³ + 1 + 6x ( 2x + 1 )

= 8x³ + 1 + 12x² + 6x

= 8x³ + 12x² + 6x + 1

So, answer = 8x³ + 12x² + 6x + 1

(ii) ( 2a - 3b )³

Solution :

We have ( 2a - 3b )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 2a )³ - ( 3b )³ - 3 × 2a × 3b ( 2a - 3b )

= 8a³ - 27b³ - 18ab ( 2a - 3b )

= 8a³ - 27b³ - 36a²b + 54ab²

So, answer = 8a³ - 27b³ - 36a²b + 54ab²

(iii) \(\displaystyle {{\left[ {\frac{3}{2}x\,+\,1} \right]}^{3}}\)

Solution :

We have \(\displaystyle {{\left[ {\frac{3}{2}x\,+\,1} \right]}^{3}}\)

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) ]

\(\displaystyle {{\left[ {\frac{3}{2}x} \right]}^{3}}\,+\,{{(\,1\,)}^{3}}\,+\,3\,\times \,\frac{3}{2}x\,\times \,1\,\left( {\frac{3}{2}x\,+\,1} \right)\)

= \(\displaystyle \frac{{27}}{8}{{x}^{3}}\,+\,1\,+\,\frac{{9x}}{2}\,\left( {\frac{3}{2}x\,+\,1} \right)\)

= \(\displaystyle \frac{{27}}{8}{{x}^{3}}\,+\,1\,+\,\frac{{27{{x}^{2}}}}{4}\,+\,\frac{{9x}}{2}\)

= \(\displaystyle \frac{{27}}{8}{{x}^{3}}\,+\,\frac{{27{{x}^{2}}}}{4}\,+\,\frac{{9x}}{2}\,+\,1\)

So, answer = \(\displaystyle \frac{{27}}{8}{{x}^{3}}\,+\,\frac{{27{{x}^{2}}}}{4}\,+\,\frac{{9x}}{2}\,+\,1\)

(iv) \(\displaystyle {{\left[ {x\,-\,\frac{2}{3}y} \right]}^{3}}\)

Solution :

We have \(\displaystyle {{\left[ {x\,-\,\frac{2}{3}y} \right]}^{3}}\)

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

\(\displaystyle {{(\,x\,)}^{3}}\,-\,{{\left[ {\frac{2}{3}y} \right]}^{3}}\,-\,3\,\times \,x\,\times \,\frac{2}{3}y\,\left( {x\,-\,\frac{2}{3}y} \right)\)

=

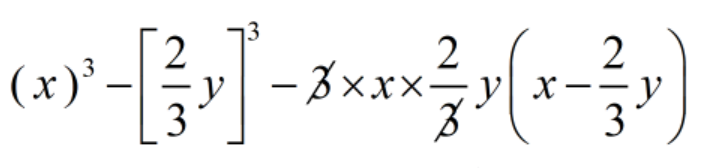
= \(\displaystyle {{x}^{3}}\,-\,\frac{8}{{27}}{{y}^{3}}\,-\,2xy\,\left( {x\,-\,\frac{2}{3}y} \right)\)

= \(\displaystyle {{x}^{3}}\,-\,\frac{8}{{27}}{{y}^{3}}\,-\,2{{x}^{2}}y\,+\,\frac{{4x{{y}^{2}}}}{3}\)

So, answer = \(\displaystyle {{x}^{3}}\,-\,\frac{8}{{27}}{{y}^{3}}\,-\,2{{x}^{2}}y\,+\,\frac{{4x{{y}^{2}}}}{3}\)

Q7. Evaluate the following using suitable identities :

(i) (99)³

Solution :

We have (99)³

( 100 - 1 )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 100 )³ - ( 1 )³ - 3 × 100 × 1 ( 100 - 1 )

= 1000000 - 1 - 300 ( 100 - 1 )

= 1000000 - 1 - 30000 + 300

= 1000300 - 30001

= 970299

So, answer = 970299

(ii) ( 102 )³

Solution :

We have ( 102 )³

( 100 + 2 )³

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) ]

( 100 )³ + ( 2 )³ + 3 × 100 × 2 ( 100 + 2 )

= 1000000 + 8 + 600 ( 100 + 2 )

= 1000000 + 8 + 60000 + 1200

= 1061208

So, answer = 1061208

(iii) ( 998 )³

Solution :

We have ( 998 )³

( 1000 - 2 )³

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 1000 )³ - ( 2 )³ - 3 × 1000 × 2 ( 1000 - 2 )

= 1000000000 - 8 - 6000 ( 1000 - 2 )

= 1000000000 - 8 - 6000000 + 12000

= 1000012000 - 6000008

= 994011992

So, answer = 994011992

Q8. Factorise each of the following :

(i) 8a³ + b³ + 12a²b + 6ab²

Solution :

We have 8a³ + b³ + 12a²b + 6ab²

[ using identity = ( x + y )³ = x³ + y³ + 3xy ( x + y ) ]

( 2a )³ + ( b )³ + 3 × 2a × b ( 2a + b )

= ( 2a + b )³

= ( 2a + b ) ( 2a + b ) ( 2a + b )

So, answer = ( 2a + b ) ( 2a + b ) ( 2a + b )

(ii) 8a³ - b³ - 12a²b + 6ab²

Solution :

We have 8a³ - b³ - 12a²b + 6ab²

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 2a )³ - ( b )³ - 3 × 2a × b ( 2a - b )

= ( 2a - b )³

= ( 2a - b ) ( 2a - b ) ( 2a - b )

So, answer = ( 2a - b ) ( 2a - b ) ( 2a - b )

(iii) 27 - 125a³ - 135a + 225a²

Solution :

We have 27 - 125a³ - 135a + 225a²

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 3 )³ - ( 5a )³ - 3 × 3 × 5a ( 3 - 5a )

= ( 3 - 5a )³

= ( 3 - 5a ) ( 3 - 5a ) ( 3 - 5a )

So, answer = ( 3 - 5a ) ( 3 - 5a ) ( 3 - 5a )

(iv) 64a³ - 27b³ - 144a²b + 108 ab²

Solution :

We have 64a³ - 27b³ - 144a²b + 108 ab²

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 4a )³ - ( 3b )³ - 3 × 4a × 3b ( 4a - 3b )

= ( 4a - 3b )³

= ( 4a - 3b ) ( 4a - 3b ) ( 4a - 3b )

So, answer = ( 4a - 3b ) ( 4a - 3b ) ( 4a - 3b )

(v) 27p³ - \(\displaystyle \frac{1}{{216}}\,-\,\frac{9}{2}{{p}^{2}}\,+\,\frac{1}{4}p\)

Solution :

We have 27p³ - \(\displaystyle \frac{1}{{216}}\,-\,\frac{9}{2}{{p}^{2}}\,+\,\frac{1}{4}p\)

[ using identity = ( x - y )³ = x³ - y³ - 3xy ( x - y ) ]

( 3p )³ - ( \(\displaystyle \frac{1}{6}\) )³ - 3 × 3p × \(\displaystyle \frac{1}{6}\) ( 3p - \(\displaystyle \frac{1}{6}\) )

= ( 3p - \(\displaystyle \frac{1}{6}\) )³

= ( 3p - \(\displaystyle \frac{1}{6}\) ) ( 3p - \(\displaystyle \frac{1}{6}\) ) ( 3p - \(\displaystyle \frac{1}{6}\) )

So, answer = ( 3p - \(\displaystyle \frac{1}{6}\) ) ( 3p - \(\displaystyle \frac{1}{6}\) ) ( 3p - \(\displaystyle \frac{1}{6}\) )

NCERT Solutions Class 9 Maths Chapter 2

 

Q9. Verify : (i) x³ + y³ = ( x + y ) ( x² - xy + y² )

Solution : 

Given  x³ + y³

LHS = x³ + y³     ,  RHS = ( x + y ) ( x² - xy + y² )

We have multiply to the first bracket by the second bracket

( x + y ) ( x² - xy + y² )

= x ( x² - xy + y² ) + y ( x² - xy + y² )

= x³ - x²y + xy² + x²y - xy² + y³    [ because - x²y + x²y = 0 , xy² - xy² = 0 ]

= x³ + y³

∴ LHS = RHS

So, proved LHS = RHS

(ii) x³ - y³ = ( x - y ) ( x² + xy + y² )

Solution :

Given x³ - y³

LHS = x³ - y³     ,  RHS = ( x - y ) ( x² + xy + y² )

We have multiply to the first bracket by the second bracket

( x - y ) ( x² + xy + y² )

= x ( x² + xy + y² ) - y ( x² + xy + y² )

= x³ + x²y + xy² - xy² - xy² - y³      [ because x²y - x²y = 0 ,  xy² - xy² = 0 ]

= x³ - y³

∴ LHS = RHS

So, proved LHS = RHS

Q10. Factorise each of the following :

(i) 27x³ + 125z³

Solution :

We have 27x³ + 125z³

( 3y )³ + ( 5z )³

= ( 3y + 5z ) ( 9y² - 15yz + 25z² )

So, answer = ( 3y + 5z ) ( 9y² - 15yz + 25z² )

(ii) 64m³ - 343n³

Solution :

We have 64m³ - 343n³

( 4m )³ - ( 7n )³

= ( 4m - 7n ) ( 16m² + 28mn + 49n² )

So, answer = ( 4m - 7n ) ( 16m² + 28mn + 49n² )

[ Hint : See Question 9. ]

Q11. Factorise : 27x³ + y³ + z³ - 9xyz

Solution :

We have 27x³ + y³ + z³ - 9xyz

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

( 3x )³ + ( y )³ + ( z )³ - 3 × ( 3x ) ( y ) ( z )

= ( 3x + y + z ) [ ( 3x )² + ( y )² + ( z )² - ( 3x )( y ) - ( y )( z ) - ( z )( 3x )

= ( 3x + y + z ) ( 9x² + y² + z² - 3xy - yz - 3xz )

So, answer = ( 3x + y + z ) ( 9x² + y² + z² - 3xy - yz - 3xz )

Q12. Verify that x³ + y³ + z³ - 3xyz = \(\displaystyle \frac{1}{2}\) ( x + y + z )

[ ( x - y )² + ( y - z )² + ( z - x )² ]

Solution : 

We have x³ + y³ + z³ - 3xyz

LHS = x³ + y³ + z³ - 3xyz ,     RHS = \(\displaystyle \frac{1}{2}\) ( x + y + z )

[ ( x - y )² + ( y - z )² + ( z - x )² ]

[ using identity = ( a - b )² = a² - 2ab + b² ]

\(\displaystyle \frac{1}{2}\) ( x + y + z ) [ ( x - y )² + ( y - z )² + ( z - x )² ]

= \(\displaystyle \frac{1}{2}\) ( x + y + z ) [ x² - 2xy + y² + y² - 2yz + z² + z² - 2xz + x² ]

= \(\displaystyle \frac{1}{2}\) ( x + y + z ) [ 2x² - 2xy + 2y² - 2yz + 2z² - 2xz ]

= \(\displaystyle \frac{1}{2}\) ( x + y + z ) × 2 [ x² - xy + y² - yz + z² - xz ]

=

= ( x + y + z ) ( x² + y² + z² - xy - yz - xz )

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

= ( x )³ + ( y )³ + ( z )³ - 3 × x × y × z

= x³ + y³ + z³ - 3xyz

∴ LHS = RHS

So, proved LHS = RHS

Q13. If x + y + z = 0 , show that x³ + y³ + z³ = 3xyz.

Solution :

We have x³ + y³ + z³ = 3xyz

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

x³ + y³ + z³ - 3xyz  = ( x + y + z ) ( x² + y² + z² - xy - yz - zx )

= x³ + y³ + z³ - 3xyz = ( 0 ) ( x² + y² + z² - xy - yz - zx )      [ put x + y + z = 0 ]

= x³ + y³ + z³ - 3xyz = 0

= x³ + y³ + z³ = 3xyz

∴ LHS = RHS

So, simplify RHS

Q14. Without actually calculating the cubes, find the value of each of the following :

(i) ( -12 )³ + ( 7 )³ + ( 5 )³

Solution :

We have ( -12 )³ + ( 7 )³ + ( 5 )³

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

Here, x = -12  , y = 7  and z = 5

( -12 )³ + ( 7 )³ + ( 5 )³ - 3xyz = 0

( -12 )³ + ( 7 )³ + ( 5 )³ = 3xyz     [ according to the above identity ]

= ( -12 )³ + ( 7 )³ + ( 5 )³ = 3 ( -12 ) ( 7 ) ( 5 ) + ( -12 + 7 + 5 ) ( -12² + 7² + 5² - ( -12 × 7 ) - ( 7 × 5 ) - ( 5 × -12 )

= ( -12 )³ + ( 7 )³ + ( 5 )³ = -1260 + ( 0 ) ( 144 + 49 + 25 + 84 - 35 + 60 )

= ( -12 )³ + ( 7 )³ + ( 5 )³ = -1260 + ( 0 )

= ( -12 )³ + ( 7 )³ + ( 5 )³ = -1260

So, answer = -1260

(ii) ( 28 )³ + ( -15 )³ + ( -13 )³

Solution :

We have ( 28 )³ + ( -15 )³ + ( -13 )³

[ using identity = x³ + y³ + z³ - 3xyz = ( x + y + z ) ( x² + y² + z² - xy - yz - zx ) ]

Here, x = 28  , y = -15  and z = -13

( 28 )³ + ( -15 )³ + ( -13 )³ - 3xyz = 0

( 28 )³ + ( -15 )³ + ( -13 )³ = 3xyz          [ according to the above identity ]

= ( 28 )³ + ( -15 )³ + ( -13 )³ = 3 ( 28 ) ( -15 ) ( -13 ) + ( 28 - 15 - 13 ) ( 28² + ( -15)² + ( -13 )² - ( 28 × -15 ) - ( -15 × -13 ) - ( -13 × 28 )

= ( 28 )³ + ( -15 )³ + ( -13 )³ = 16380 + ( 0 ) ( 784 + 225 + 169 + 420 - 195 + 364 )

= ( 28 )³ + ( -15 )³ + ( -13 )³ = 16380 + ( 0 )

= ( 28 )³ + ( -15 )³ + ( -13 )³ = 16380

So, answer = 16380

Note:- you will found Answer in -ve (in your Book) so Don't worry above answer is Correct.

Q15. Give possible expressions for the length and breadth of each of the following rectangle, in which their areas are given :

(i) Area : 25a² - 35a + 12

Solution :

Given 25a² - 35a + 12

[ Using the splitting the middle term method ]

So, 25a² - 35a + 12

= 25a² - 20a - 15a + 12

= 5a ( 5a - 4 ) - 3 ( 5a - 4 )

= ( 5a - 3 ) ( 5a - 4 )

∴ Length = ( 5a - 3 ) , Breadth = ( 5a - 4 )

(ii) Area : 35y² + 13y - 12

Solution :

Given 35y² + 13y - 12

[ Using the splitting the middle term method ]

So, 35y² + 13y - 12

= 35y² + 28y - 15y - 12

= 7y ( 5y + 4 ) - 3 ( 5y + 4 )

= ( 7y - 3 ) ( 5y + 4 )

∴ Length = ( 7y - 3 ) , Breadth = ( 5y + 4 )

Q16. What are the possible expression for the dimension of the cuboids whose volumes are given below ?

(i) Volume : 3x³ - 12x

Solution :

Given 3x³ - 12x

3x³ - 12x     [ find the common ]

= ( 3 ) ( x ) ( x - 4 )

∴ Length = 3 , Breadth = x and Height = ( x - 4 )

(ii) Volume : 12ky² + 8ky - 20k

Solution : 

Given 12ky² + 8ky - 20k

12ky² + 8ky - 20k          [ find the common ]

= 4k ( 3y² + 2y - 5 )

[ Using the splitting the middle term method ]

So, 4k ( 3y² + 2y - 5 )

= 4k ( 3y² + 5y - 3y - 5 )     [ find the common ]

= ( 4k ) [ ( y ( 3y + 5 ) - 1 ( 3y + 5 ) ]

= ( 4k ) ( y - 1 ) ( 3y + 5 )

∴ Length = 4k , Breadth = ( y - 1 ) and Height = ( 3y + 5 ) .

 

NCERT Class 9 Maths Chapter 2 Polynomials :

• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.1
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.2
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.3
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.4
• NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.5