NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Leave a Comment / Class 9 Maths, Class 8 Maths Chapter 9, Class 9 Maths Chapter 2 / By eGuru

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Introduction:

In this exercise/article we will learn about multiplication of algebraic expression. Multiplying a monomials by a monomials and multiply two monomials and multiplying three or more monomials find out factor of monomials. [ using identity = volume of rectangle = Length × Breadth × Height ] only on using formula and multiply do in this exercise .

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

Class 8 Maths Exercise 9.2 (Page-143)

Q1. Find the product of the following pairs of monomials.

(i) 4 , 7p

Solution :

We have 4 , 7p

we know very well

= 4 × 7p

= 28p

So, answer is 28p

(ii) - 4p , 7p

Solution :

We have - 4p , 7p

we know very well

= - 4p × 7p

= - 28p²

So, answer is - 28p²

(iii) - 4p , 7pq

Solution :

We have - 4p , 7pq

we know very well

= - 4p × 7pq

= - 28p²q

So, answer is - 28pq

(iv) 4p³ , - 3p

Solution :

We have 4p³ , - 3p

we know very well

= 4p³ × - 3p

= - 12p⁴

So, answer is - 12p⁴

(v) 4p , o

Solution :

We have 4p , o

we know very well

= 4p × o

= 0

So, answer is 0

Q2. Find the area of rectangles with the following of monomials as their lengths and breadths respectively.

( p , q ) ; ( 10m , 5n ) ; ( 20x² , 5y² ) ; ( 4x , 3x² ) ; ( 3mn , 4np )

Solution :

We have given ( p , q )

here, Length = p, breadth = q

Area of rectangle = length × breadth

= p × q

= pq

We have given ( 10m , 5n )

here, Length = 10m, breadth = 5n

Area of rectangle = length × breadth

= 10m × 5n

= 50mn

We have given ( 20x² , 5y² )

here, Length = 20x², breadth = 5y²

Area of rectangle = length × breadth

= 20x² × 5y²

= 100x²y²

We have ( 4x , 3x² )

here, Length = 4x, breadth = 3x²

Area of rectangle = length × breadth

= 4x × 3x²

= 12x³

We have ( 3mn , 4np )

here, Length = 3mn, breadth = 4np

Area of rectangle = length × breadth

= 3mn × 4np

= 12mn²p

Class 8 Maths Chapter 9 Exercise 9.2

Q3. Complete the table products.

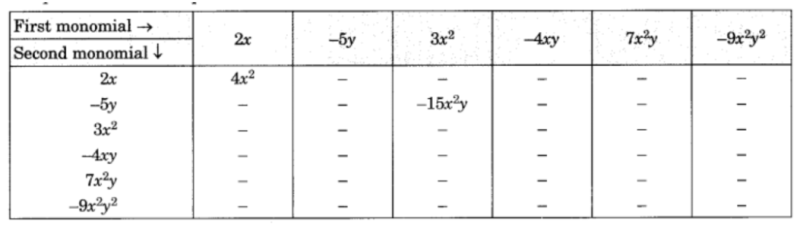
Solution :

Multiply the first monomial by the second monomials

Q4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.

(i) 5a, 3a² , 7a⁴

Solution :

We have 5a, 3a² , 7a⁴

here, Length = 5a, breadth = 3a² and height = 7a⁴

Volume of rectangle = length × breadth × height

= 5a × 3a² × 7a⁴

= 105a⁷

So, answer is 105a⁷

(ii) 2p, 4q, 8r

Solution :

We have 2p, 4q, 8r

here, Length = 2p, breadth = 4q and height = 8r

Volume of rectangle = length × breadth × height

= 2p × 4q × 8r

= 64pqr

So, answer is 64pqr

(iii) xy, 2x²y, 2xy²

Solution :

We have xy, 2x²y, 2xy²

here, Length = xy, breadth = 2x²y and height = 2xy²

Volume of rectangle = length × breadth × height

= xy × 2x²y × 2xy²

= 4x⁴y⁴

So, answer is 4x⁴y⁴

(iv) a, 2b, 3c

Solution :

We have a, 2b, 3c

here, Length = a, breadth = 2b and height = 3c

Volume of rectangle = length × breadth × height

= a × 2b × 3c

= 6abc

So, answer is 6abc

Q5. Obtain the product of

(i) xy, yz, zx

Solution :

We have xy, yz, zx

multiply all these

= xy × yz × zx

= x²y²z²

So, answer is x²y²z²

(ii) a, - a² , a³

Solution :

We have a, - a² , a³

multiply all these

= a × - a² × a³

= - a⁶

So, answer is - a⁶

(iii) 2, 4y, 8y², 16y³

Solution :

We have 2, 4y, 8y², 16y³

multiply all these

= 2 × 4y × 8y² × 16y³

= 1024y⁶

So, answer is 1024y⁶

(iv) a, 2b, 3c, 6abc

We have a, 2b, 3c, 6abc

multiply all these

= a × 2b × 3c × 6abc

= 36a²b²c²

= So, answer is 36a²b²c²

(v) m, - mn, mnp

Solution :

We have m, - mn, mnp

multiply all these

= m × - mn × mnp

= - m³n²p

So, answer is - m³n²p .

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

Leave a Comment Cancel Reply