Spread the love

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.5

Introduction:

In this exercise/article we will learn about multiplication of algebraic expressions. [ using identity = ( a + b )² = a² + 2ab + b² and ( a - b )² = a² - 2ab + b² and ( x + a ) ( x + b ) = x² + ( a + b ) x + ab and ( a - b ) ( a + b ) = a² - b² you learn identity before then do this exercise. In all question put on identity.

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

Class 8 Maths Exercise 9.5 (Page-151)

Q1. Use a suitable identity to get each of the following products.

(i) ( x + 3 ) ( x + 3 )

Solution :

We have ( x + 3 ) ( x + 3 ) = ( x + 3 )²

= ( x + 3 )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here a = x and b = 3

So that,

( x )² + 2 × x × 3 + ( 3 )²

= x² + 6x + 9

So, answer is x² + 6x + 9

(ii) ( 2y + 5 ) ( 2y + 5 )

Solution :

We have ( 2y + 5 ) ( 2y + 5 ) = ( 2y + 5 )²

= ( 2y + 5 )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here, a = 2y and b = 5

So that,

( 2y )² + 2 × 2y × 5 + ( 5 )²

= 4y² + 20y + 25

So, answer is 4y² + 20y + 25

(iii) ( 2a - 7 ) ( 2a - 7 )

Solution :

We have ( 2a - 7 ) ( 2a - 7 ) = ( 2a - 7 )²

= ( 2a - 7 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 2a and b = 7

So that,

( 2a )² - 2 × 2a × 7 + ( 7 )²

= 4a² - 28a + 49

So, answer is 4a² - 28a + 49

(iv) \(\displaystyle (\,3a\,-\,\frac{1}{2}\,)\,(\,3a\,-\,\frac{1}{2}\,)\)

Solution :

We have \(\displaystyle (\,3a\,-\,\frac{1}{2}\,)\,(\,3a\,-\,\frac{1}{2}\,)\)\(\displaystyle ={{(\,3a\,-\,\frac{1}{2}\,)}^{2}}\)

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 3a and b = \(\displaystyle \frac{1}{2}\)

So that,

( 3a )² - 2 × 3a × \(\displaystyle \frac{1}{2}\) + ( \(\displaystyle \frac{1}{2}\) )²

= 9a² - 3a + \(\displaystyle \frac{1}{4}\)

So, answer is 9a² - 3a + \(\displaystyle \frac{1}{4}\)

(v) ( 1.1m - 0.4 ) ( 1.1m + 0.4 )

We have ( 1.1m - 0.4 ) ( 1.1m + 0.4 )

[ using identity = ( a - b ) ( a + b ) = a² - b² ]

Here, a = 1.1m and b = 0.4

( 1.1m )² - ( 0.4 )²

= 1.21m² - 0.16

So, answer is 1.21m² - 0.16

(vi) ( a² + b² ) ( - a² + b² )

Solution :

We have ( a² + b² ) ( - a² + b² )

[ we have multiply to the first bracket by the second bracket ]

a²( - a² + b² ) + b² ( - a² + b² )

= - a⁴ + a²b² - a²b² + b⁴ [ because ( a²b² - a²b² ) = 0 ]

= b⁴ - a⁴

So, answer is b⁴ - a⁴

(vii) ( 6x - 7 ) ( 6x + 7 )

Solution :

We have ( 6x - 7 ) ( 6x + 7 )

[ using identity = ( a - b ) ( a + b ) = a² - b² ]

Here, a = 6x and b = 7

So that,

( 6x )² - ( 7 )²

= 36x² - 49

So, answer is 36x² - 49

(viii) ( - a + c ) ( - a + c )

Solution :

We have ( - a + c ) ( - a + c ) = ( - a + c )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here, a = - a and b = c

So that,

( - a )² + 2 × - a × c + ( c )²

= a² - 2ac + c²

So, answer is a² - 2ac + c²

(ix) \(\displaystyle \left( {\frac{x}{2}\,+\,\frac{{3y}}{4}} \right)\) \(\displaystyle \left( {\frac{x}{2}\,+\,\frac{{3y}}{4}} \right)\)

Solution :

We have \(\displaystyle \left( {\frac{x}{2}\,+\,\frac{{3y}}{4}} \right)\) \(\displaystyle \left( {\frac{x}{2}\,+\,\frac{{3y}}{4}} \right)\) = \(\displaystyle {{\left( {\frac{x}{2}+\frac{{3y}}{4}} \right)}^{2}}\)

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here, a = \(\displaystyle {\frac{x}{2}}\) and b = \(\displaystyle {\frac{{3y}}{4}}\)

So that,

= \(\displaystyle {{\left( {\frac{x}{2}} \right)}^{2}}\,+\,2\,\times \,\frac{x}{2}\,\times \,\frac{{3y}}{4}\,+\,{{\left( {\frac{{3y}}{4}} \right)}^{2}}\)

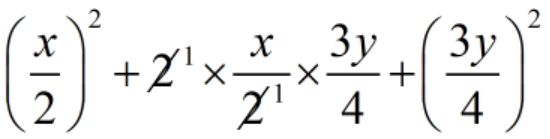
= \(\displaystyle \frac{{{{x}^{2}}}}{4}\,+\,\frac{{3xy}}{4}\,+\,\frac{{9{{y}^{2}}}}{{16}}\)

So, answer is \(\displaystyle \frac{{{{x}^{2}}}}{4}\,+\,\frac{{3xy}}{4}\,+\,\frac{{9{{y}^{2}}}}{{16}}\)

(x) ( 7a - 9b ) ( 7a - 9b )

Solution :

We have ( 7a - 9b ) ( 7a - 9b ) = ( 7a - 9b )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 7a and b = 9b

So that,

( 7a )² - 2 × 7a × 9b + ( 9b )²

= 49a² - 126ab + 81b²

So, answer is 49a² - 126ab + 81b²

Q2. Use the identity ( x + a ) ( x + b ) = x² + ( a + b ) x + ab to find the following products.

(i) ( x + 3 ) ( x + 7 )

Solution :

We have ( x + 3 ) ( x + 7 )

[ using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = x , a = 3 and b = 7

So that,

( x )² + ( 3 + 7 ) x + 3 × 7

= x²+ ( 10 ) x + 21

= x²+ 10 × x + 21

= x²+10x +21

So, answer is x²+10x +21

(ii) ( 4x + 5 ) ( 4x + 1 )

Solution :

We have ( 4x + 5 ) ( 4x + 1 )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 4x , a = 5 and b = 1

So that,

( 4x )² + ( 5 + 1 ) 4x + 5 × 1

= 16x² + ( 6 ) 4x + 5

= 16x² + 6 × 4x + 5

= 16x² + 24x + 5

So, answer is 16x² + 24x + 5

(iii) ( 4x - 5 ) ( 4x - 1 )

We have ( 4x - 5 ) ( 4x - 1 )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 4x , a = - 5 and b = -1

So that,

[( 4x )² + {( - 5 ) + ( -1 )} 4x + ( - 5 ) × ( - 1 )]

= 16x² + (- 6) 4x + ( 5 )

= 16x² - 6 × 4x + 5

= 16x² - 24x + 5

So, answer is 16x² - 24x + 5

(iv) ( 4x + 5 ) ( 4x - 1 )

Solution :

We have ( 4x + 5 ) ( 4x - 1 )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 4x , a = 5 and b = - 1

So that,

[( 4x )² + { 5 + ( -1 ) } 4x + 5 × ( - 1 )]

= 16x² ( 4 ) 4x - 5

= 16x² + 4 × 4x - 5

= 16x² + 16x - 5

So, answer is 16x² + 16x - 5

(v) ( 2x + 5y ) ( 2x + 3y )

Solution :

We have ( 2x + 5y ) ( 2x + 3y )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 2x , a = 5y and b = 3y

So that,

( 2x )² + ( 5y + 3y ) 2x + 5y × 3y

= 4x² + ( 8y ) 2x + 15y²

= 4x² + 8y × 2x + 15y²

= 4x² + 16xy + 15y²

So, answer is 4x² + 16xy + 15y²

(vi) ( 2a² + 9 ) ( 2a² + 5 )

We have ( 2a² + 9 ) ( 2a² + 5 )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 2a² , a = 9 and b = 5

So that,

( 2a )² + ( 9 + 5 ) 2a² + 9 × 5

= 4a⁴ + ( 14 ) 2a² + 45

= 4a⁴ + 14 × 2a² + 45

= 4a⁴ + 28a² + 45

So, answer is 4a⁴ + 28a² + 45

(vii) ( xyz - 4 ) ( xyz - 2 )

Solution :

We have ( xyz - 4 ) ( xyz - 2 )

[ using identity = [( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = xyz , a = - 4 and b = - 2

So that,

[( xyz )² + { ( - 4 ) + ( - 2 ) } xyz + ( - 4 × - 2 )]

= x²y²z² + ( - 6 ) xyz + 8

= x²y²z² - 6 × xyz + 8

= x²y²z² - 6xyz + 8

So, answer is x²y²z² - 6xyz + 8

Q3. Find the following squares by using the identities.

(i) ( b - 7 )²

Solution :

We have ( b - 7 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here , a = b and b = 7

So that,

b² - 2 × b × 7 + 7²

= b² - 14b + 49

So, answer is b² - 14b + 49

(ii) ( xy + 3z )²

Solution :

We have ( xy + 3z )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here , a = xy and b = 3z

So that,

( xy )² + 2 × xy × 3z + ( 3z )²

= xy² + 6xyz + 9z²

So, answer is xy² + 6xyz + 9z²

(iii) ( 6x² - 5y )²

Solution :

We have ( 6x² - 5y )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here , a = 6x² and b = 5y

So that,

( 6x² ) - 2 × 6x² × 5y + ( 5y )²

= 36x² - 60x²y + 5y²

So, answer is 36x² - 60x²y + 5y²

(iv) \(\displaystyle {{\left( {\frac{2}{3}m\,+\,\frac{3}{2}n} \right)}^{2}}\)

Solution :

We have \(\displaystyle {{\left( {\frac{2}{3}m\,+\,\frac{3}{2}n} \right)}^{2}}\)

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here , a = \(\displaystyle {\frac{2}{3}m}\) and b = \(\displaystyle {\frac{3}{2}n}\)

So that,

= \(\displaystyle {{\left( {\frac{2}{3}m} \right)}^{2}}\,+\,2\,\times \,\frac{2}{3}m\,\times \,\frac{3}{2}n\,+\,{{\left( {\frac{3}{2}n} \right)}^{2}}\)

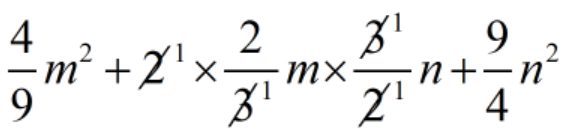
= \(\displaystyle \frac{4}{9}{{m}^{2}}\,+\,2mn\,+\,\frac{9}{4}{{n}^{2}}\)

So, answer is \(\displaystyle \frac{4}{9}{{m}^{2}}\,+\,2mn\,+\,\frac{9}{4}{{n}^{2}}\)

(v) ( 0.4p - 0.5q )²

Solution :

We have ( 0.4p - 0.5q )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here , a = 0.4p and b = 0.5q

So that,

( 0.4p )² + 2 × 0.4p × 0.5q + ( 0.5q )²

= 0.16p² + 0.4pq + 0.25q²

So, answer is 0.16p² + 0.4pq + 0.25q²

(vi) ( 2xy + 5y )²

Solution :

We have ( 2xy + 5y )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here , a = 2xy and b = 5y

So that,

( 2xy )² + 2 × 2xy × 5y + ( 5y )²

= 4x²y² + 20xy² + 25y²

So, answer is 4x²y² + 20xy² + 25y²

Class 8 Maths Chapter 9 Exercise 9.5

Q4. Simplify.

(i) ( a² - b² )²

Solution :

We have ( a² - b² )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here , a = a² and b = b²

So that,

( a² )² - 2 × a² × b² + ( b² )²

= a⁴ - 2a²b² + b⁴

So, answer is a⁴ - 2a²b² + b⁴

(ii) ( 2x + 5 )² - ( 2x - 5 )²

Solution :

We have ( 2x + 5 )² - ( 2x - 5 )²

[ using identity = ( a + b )² = a² + 2ab + b² and ( a - b )² = a² - 2ab + b² ]

Here , a = 2x and b = 5 and a = 2x and b = 5

So that,

[ { ( 2x )² + 2 × 2x × 5 + ( 5 )² } - { ( 2x )² - 2 × 2x × 5 + ( 5 )² } ]

= ( 2x )² + 2 × 2x × 5 + ( 5 )² - ( 2x )² + 2 × 2x × 5 - ( 5 )²

= 4x² + 20x + 25 - 4x² + 20x - 25 [ because = 4x² - 4x² = 0 and 25 - 25 = 0 ]

= 40x

So, answer is 40x

(iii) ( 7m - 8n )² + ( 7m + 8n )²

Solution :

We have ( 7m - 8n )² + ( 7m + 8n )²

[ using identity = ( a - b )² = a² - 2ab + b² and ( a + b )² = a² + 2ab + b² ]

Here , a = 7m and b = 8n and a = 7m and b = 8n

So that,

[ { ( 7m )² - 2 × 7m × 8n + ( 8n )² } +{ ( 7m )² + 2 × 7m × 8n + ( 8n )² } ]

= ( 7m )² - 2 × 7m × 8n + ( 8n )² + ( 7m )² + 2 × 7m × 8n + ( 8n )²

= 49m² - 112mn + 64n² + 49m² + 112mn + 64n² [ because = - 112mn + 112mn = 0 ]

= ( 49m² + 49m² ) ( 64n² + 64n² )

= 98m² + 128n²

So, answer is 98m² + 128n²

(vi) ( 4m + 5n )² + ( 5m + 4n )²

Solution :

We have ( 4m + 5n )² + ( 5m + 4n )²

[ using identity = ( a + b )² = a² + 2ab + b² and ( a + b )² = a² + 2ab + b² ]

Here , a = 4m and b = 5n and a = 5m and b = 4n

So that,

( 4m )² + 2 × 4m × 5n + ( 5n )² + ( 5m )² + 2 × 5m × 4n + ( 4n )²

= 16m² + 40mn + 25n² + 25m² + 40mn + 16n²

= ( 16m² + + 25m² ) ( 40mn + 40mn ) ( 25n² + 16n² )

= 41m² + 80mn + 41n²

So, answer is 41m² + 80mn + 41n²

(v) ( 2.5p - 1.5q )² - ( 1.5p - 2.5q )²

Solution :

We have ( 2.5p - 1.5q )² - ( 1.5p - 2.5q )²

[ using identity = ( a - b )² = a² - 2ab + b² and ( a - b )² = a² - 2ab + b² ]

Here , a = 2.5p and b = 1.5q and a = 1.5p and b = 2.5q

So that,

[{ ( 2.5p )² - 2 × 2.5p × 1.5q + ( 1.5q )² } - { ( 1.5p )² - 2 × 1.5q × 2.5p + ( 2.5q )² }]

= 6.25p² - 7.5pq + 2.25q² - 2.25p² + 7.5pq - 6.25q² [ because = - 7.5pq + 7.5pq = 0 ]

= ( 6.25p² - 2.25p² ) - ( 2.25q² - 6.25q² )

= 4p² - 4q²

So, answer is 4p² - 4q²

(vi) ( ab + bc )² - 2ab²c

Solution :

We have ( ab + bc )² - 2ab²c

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here , a = ab and b = bc

So that,

( ab )² + 2 × ab × bc + ( bc )² - 2ab²c

= a²b² + 2ab²c + b²c² - 2ab²c [ because = 2ab²c - 2ab²c = 0 ]

= a²b² + b²c²

So, answer is a²b² + b²c²

(vii) ( m² - n²m )² + 2m³n²

Solution :

We have ( m² - n²m )² + 2m³n²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here , a = m² and b = n²m

So that,

( m² )² - 2 × m² × n²m + ( n²m )² + 2m³n²

= m⁴ - 2m³n² + n⁴m² + 2m³n² [ because = - 2m³n² + 2m³n² = 0 ]

= m⁴ + n⁴m²

So, answer is m⁴ + n⁴m²

Q5. Show that.

(i) ( 3x + 7 )² - 84x = ( 3x - 7 )²

Solution :

We have ( 3x + 7 )² - 84x = ( 3x - 7 )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

LHS = ( 3x + 7 )² - 84x = RHS = ( 3x - 7 )²

= ( 3x )² + 2 × 3x × 7 + ( 7 ) - 84x

= 9x² + 42x + 49 - 84x [ because = 42x - 84x = - 42 ]

= 9x² - 42x + 49

= ( 3x - 7 )² = ( 3x - 7 )²

= LHS = RHS

Hence proved

(ii) ( 9p - 5q )² + 180pq = ( 9p + 5q )²

Solution :

We have ( 9p - 5q )² + 180pq = ( 9p + 5q )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

LHS = ( 9p - 5q )² + 180pq = RHS = ( 9p + 5q )²

( 9p )² - 2 × 9p × 5q + ( 5q )² + 180pq

81p² - 90pq + 25q² + 180pq [ because = - 90pq + 180pq = 0 ]

= 81p² + 90pq + 25q²

= ( 9p + 5q )² = ( 9p + 5q )²

= LHS = RHS

Hence proved

(iii) \(\displaystyle {{\left( {\frac{4}{3}m\,-\,\frac{3}{4}n} \right)}^{2}}\,+\,2mn\,=\,\frac{{16}}{9}{{m}^{2}}\,+\,\frac{9}{{16}}{{n}^{2}}\)

Solution :

We have \(\displaystyle {{\left( {\frac{4}{3}m\,-\,\frac{3}{4}n} \right)}^{2}}\,+\,2mn\,=\,\frac{{16}}{9}{{m}^{2}}\,+\,\frac{9}{{16}}{{n}^{2}}\)

[ using identity = ( a - b )² = a² - 2ab + b² ]

LHS = \(\displaystyle {{\left( {\frac{4}{3}m\,-\,\frac{3}{4}n} \right)}^{2}}\,+\,2mn\) = RHS = \(\displaystyle \frac{{16}}{9}{{m}^{2}}\,+\,\frac{9}{{16}}{{n}^{2}}\)

\(\displaystyle {{\left( {\frac{4}{3}m} \right)}^{2}}\,-\,2\,\times \,\frac{4}{3}m\,\times \,\frac{3}{4}n\,+\,{{\left( {\frac{3}{4}n\,} \right)}^{2}}\,+\,2mn\)

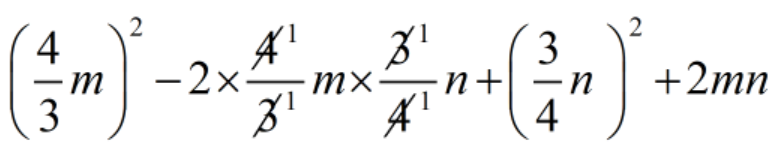
= \(\displaystyle \frac{{16}}{9}{{m}^{2}}\,-\,2mn\,+\,\frac{9}{{16}}{{n}^{2}}\,+\,2mn\) [ because = \(\displaystyle -\,2mn\) + \(\displaystyle \,2mn\) = 0 ]

= \(\displaystyle \frac{{16}}{9}{{m}^{2}}\,+\,\frac{9}{{16}}{{n}^{2}}\,\) = \(\displaystyle \frac{{16}}{9}{{m}^{2}}\,+\,\frac{9}{{16}}{{n}^{2}}\,\)

= LHS = RHS

Hence proved

(iv) ( 4pq + 3q )² - ( 4pq - 3q )² = 48pq²

Solution :

We have ( 4pq + 3q )² - ( 4pq - 3q )² = 48pq²

[ using identity = ( a + b )² = a² + 2ab + b² and ( a - b )² = a² - 2ab + b² ]

LHS = ( 4pq + 3q )² - ( 4pq - 3q )² = RHS = 48pq²

[{ ( 4pq )² + 2 × 4pq × 3q + ( 3q )² } - { ( 4pq )² - 2 × 4pq × 3q + ( 3q )² }]

= 16p²q² + 24pq² + 9q² - 16p²q² + 24pq² - 9q² [ because = 16p²q² - 16p²q² = o and 9q² - 9q² = 0 ]

= 48pq² = 48pq²

= LHS = RHS

Hence proved

(v) ( a - b ) ( a + b ) + ( b - c ) ( b + c ) + ( c - a ) ( c + a ) = 0

Solution :

We have ( a - b ) ( a + b ) + ( b - c ) ( b + c ) + ( c - a ) ( c + a ) = 0

[ we have to the multiply the first bracket by the second bracket ]

a ( a + b ) - b ( a + b ) + b ( b + c ) - c ( b + c ) + c ( c + a ) - a ( c + a ) = 0

= a² + ab - ab - b² + b² + bc - bc - c² + c² + ac - ac - a² = 0

= ( a² - a² ) ( ab - ab ) ( - b² + b² ) ( bc - bc ) ( - c² + c² ) ( ac - ac ) = 0

= ( 0 ) ( 0 ) ( 0 ) ( 0 ) ( 0 ) ( 0 ) = 0

= 0 = 0

= LHS = RHS

Hence proved

Q6. Using identities evaluate.

(i) 71²

Solution :

We have 71² = ( 70 + 1 )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here, a = 70 and b = 1

So that,

( 70 )² + 2 × 70 × 1 + ( 1 )²

= 4900 + 140 + 1

= 5041

So, answer is 5041

(ii) 99²

Solution :

We have 99² = ( 100 - 1 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 100 and b = 1

So that,

( 100 )² - 2 × 100 × 1 + ( 1 )²

= 10000 - 200 + 1

= 9800 + 1

= 9801

So, answer is 9801

(iii) 102²

Solution :

We have 102² = ( 100 + 2 )²

[ using identity = ( a + b )² = a² + 2ab + b² ]

Here, a = 100 and b = 2

So that,

( 100 )² + 2 × 100 × 2 + ( 2 )²

= 10000 + 400 + 4

= 10404

So, answer is 10404

(iv) 998²

Solution :

We have 998² = ( 1000 - 2 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 1000 and b = 2

So that,

( 1000 )² - 2 × 1000 × 2 + ( 2 )²

= 1000000 - 4000 + 4

= 996000 + 4

= 996004

So, answer is 996004

(v) 5.2²

We have 5.2² = ( 5 + 0.2 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 5 and b = 0.2

So that,

( 5 )² + 2 × 5 × 0.2 + ( 0.2 )²

= 25 + 2 + 0.04

= 27.04

So, answer is 27.04

(vi) 297 × 303

Solution :

We have 297 × 303 = ( 300 - 3 ) ( 300 + 3 )

[ using identity = ( a - b ) ( a + b ) = a² - b² ]

Here, a = 300 and b = 3

So that,

( 300 )² - ( 3 )²

= 90000 - 9

= 89991

So, answer is 89991

(vii) 78 × 82

Solution :

We have 78 × 82 = ( 80 - 2 ) ( 80 + 2 )

[ using identity = ( a - b ) ( a + b ) = a² - b² ]

Here, a = 80 and b = 2

So that,

( 80 )² - ( 2 )²

= 6400 - 4

= 6396

So, answer is 6396

(viii) 8.9²

Solution :

We have 8.9² = ( 9 - 0.1 )²

[ using identity = ( a - b )² = a² - 2ab + b² ]

Here, a = 9 and b = 0.1

So that,

( 9 )² - 2 × 9 × 0.1 + ( 0.1 )

= 81 - 1.8 + 0.01

= 79.2 + 0.01

= 79.21

So, answer is 79.21

(ix) 10.5 × 9.5

Solution :

We have 10.5 × 9.5 = ( 10 + 0.5 ) ( 10 - 0.5 )

[ using identity = ( a - b ) ( a + b ) = a² - b² ]

Here, a = 10 and b = 0.5

So that,

( 10 )² - ( 0.5 )²

= 100 - 0.25

= 99.75

So, answer is 99. 75

Q7. Using a² - b² = ( a + b ) ( a - b ), find

(i) 5l² - 49²

Solution :

We have 51² - 49²

[ using identity = a² - b² = ( a + b ) ( a - b ) ]

Here, a = 51 and b = 49

So that,

( 51 + 49 ) ( 51 - 49 )

= ( 100 ) ( 2 )

= 100 × 2

= 200

So, answer is 200

(ii) ( 1.02 )² - ( 0.98 )²

Solution :

We have ( 1.02 )² - ( 0.98 )²

[ using identity = a² - b² = ( a + b ) ( a - b ) ]

Here, a = 1.02 and b = 0.98

So that,

( 1.02 + 0.98 ) ( 1.02 - 0.98 )

= ( 2 ) ( 0.04 )

= 2 × 0.04

= 0.08

So, answer is 0.08

(iii) 153² - 147²

Solution :

We have 153² - 147²

[ using identity = a² - b² = ( a + b ) ( a - b ) ]

Here, a = 153 and b = 147

So that,

( 153 + 147 ) ( 153 - 147 )

= ( 300 ) ( 6 )

= 300 × 6

= 1800

So, answer is 1800

(iv) 12.1² - 7.9²

Solution :

We have 12.1² - 7.9²

[ using identity = a² - b² = ( a + b ) ( a - b ) ]

Here, a = 12.1 and b = 7.9

So that,

( 12.1 + 7.9 ) ( 12.1 - 7.9 )

= ( 20 ) ( 4.2 )

= 20 × 4.2

= 84

So, answer is 84

Q8. Using ( x + a ) ( x + b ) = x² + ( a + b ) x + ab, find

(i) 103 × 104

Solution :

We have 103 × 104

( 100 + 3 ) ( 100 + 4 )

[ using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 100 , a = 3 and b = 4

So that,

( 100 )² + ( 3 + 4 ) 100 + 3 × 4

= 10000 + ( 7 ) 100 + 12

= 10000 + 7 × 100 + 12

= 10000 + 700 + 12

= 10712

So, answer is 10712

(ii) 5.1 × 5.2

Solution :

We have 5.1 × 5.2

( 5 + 0.1 ) ( 5 + 0.2 )

[ using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 5 , a = 0.1 and b = 0.2

So that,

( 5 )² + ( 0.1 + 0.2 ) 5 + 0.1 × 0.2

= 25 + ( 0.3 ) 5 + 0.02

= 25 + 1.5 + 0.02

= 26.57

So, answer is 26.57

(iii) 103 × 98

Solution :

We have 103 × 98

( 100 + 3 ) ( 100 - 2 )

[ using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 100 , a = 3 and b = 2

So that,

( 100 )² + ( 3 - 2 )100 + 3 × ( - 2 )

= 10000 + 1 × 100 - 6

= 10000 + 100 - 6

= 10100 - 6

= 10094

So, answer is 10094

(iv) 9.7 × 9.8

Solution :

We have 9.7 × 9.8

( 10 - 0.3 ) ( 10 - 0.2 )

[ using identity = ( x + a ) ( x + b ) = x² + ( a + b ) x + ab ]

Here, x = 10 , a = 0.3 and b = 0.2

So that,

( 10 )² + ( - 0.3 - 0.2 )10 + ( - 0.3 ) × ( - 0.2 )

= 100 - 0.5 × 10 + 0.06

= 100 - 5 + 0.06

= 100.06 - 5

= 95.06

So, answer is 95.06 .

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.5

Introduction:

Class 8 Maths Exercise 9.5 (Page-151)

Class 8 Maths Chapter 9 Exercise 9.5

Leave a Comment Cancel Reply