Spread the love

NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3

Introduction

In this chapter 3 exercise 3.3,understanding quadrilaterals, you will come to know about the properties of angles of a parallelogram.

• The opposite angles of a parallelogram are of equal measure.

• The adjacent angles in a parallelogram are supplementary.

The diagonals of a parallelogram, in general are not of equal length. However, the diagonals of a parallelogram have an interesting property i.e the diagonals of a parallelogram bisect each other.

NCERT Class 8 Maths Chapter 3 Understanding Quadrilaterals :

NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3

Q1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.

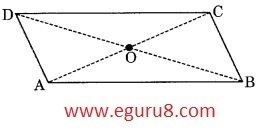
(i) AD = ........

(ii) ∠DCB = .......

(iii) OC = ........

(iv) m∠DAB + m∠CDA = ........

Solution:

(i) AD = BC [Opposite sides are equal]

(ii) ∠DCB = ∠DAB [Opposite angles are equal]

(iii) OC = OA [Diagonals bisect each other]

(iv) m∠DAB + m∠CDA = 180° [Adjacent angles are supplementary]

Q2. Consider the following parallelograms. Find the values of the unknowns x, y, z.

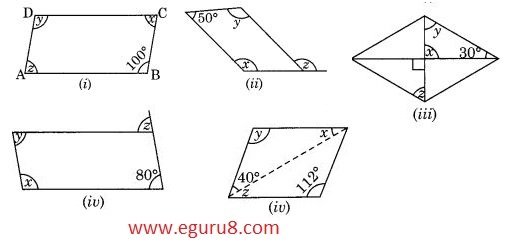
Solution:

i) ∠B = ∠D( opposite angles are equal)

so, y = 100°

∠A + ∠B = 180°( adjacent angles are supplementary)

so, z = 180° - 100°

z = 80°

∠A = ∠C (opposite angles are equal.)

so, x = 80°

Hence the value of x, y and z is 80°, 100° and 80° respectively.

ii) 50° + y = 180°(adjacent angles are supplementary)

so, y = 180° - 50°

= 130°

x = y (opposites angles are equal)

so, x = 130°

x = z ( they are corresponding angles)

so, z = 130°

Hence the value of all three x, y and is 130°.

iii) ∠x = 90°( vertically opposites angles)

∠x + ∠y + 30° = 180°( angle sum property of triangle)

90° +∠y +30° = 180°

∠y = 180° - 120°

∠y = 60°

∠z = ∠y (alternate angles)

s0, ∠z = 60°

Hence, the value of x, y and z is 90°, 60° and 60°.

iv) ∠y = 80° (opposite angles are equal)

∠y + ∠x = 180°( adjacent angles are supplementary)

80° + ∠x = 180°

∠x = 180° - 80°

∠x = 100°

∠z = ∠y (they are corresponding angles)

so, ∠z = 80°

Hence the value of x, y and z is 100°, 80° and 80° respectively.

v) ∠y = 112°( opposite angles are equal)

∠y + ∠x + 40° = 180°(angle sum property of triangle)

112° + ∠x + 40° = 180°

∠x + 152° = 180°

∠x = 180° - 152°

∠x = 28°

∠z = ∠x (alternate angles are equal)

so, ∠z = 28°

Hence, the value of x, y and z is 28°, 112° and 28° respectively.

Q3. Can a quadrilateral ABCD be a parallelogram if

(i) ∠D + ∠B = 180°?

(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?

(iii) ∠A = 70° and ∠C = 65°?

Solution:

i) A quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°, only when ∠D + ∠B = 90°(as in parallelogram, the opposites angles are equal and for that ∠D and ∠B should be of 90°).

ii) In this case a quadrilateral ABCD cannot be a parallelogram because its opposites sides are not equal.

iii) In this case a quadrilateral ABCD cannot be a parallelogram because its opposites angles are not equal.

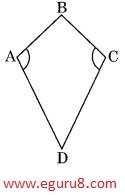
Q4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

Solution: The figure can be a kite as it is not a parallelogram but has exactly two opposite angles of equal measure.

Q5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.

Solution: Let one angle be 3x and another angle be 2x

As we know that sum of adjacent angle is 180°( adjacent angle of parallelogram is supplementary)

So, 3x + 2x = 180°

5x = 180°

x = \(\displaystyle \frac{{180{}^\circ }}{5}\)

x = 36°

s0, 3x = 3 \(\displaystyle \times \) 36 = 108°

2x = 2\(\displaystyle \times \) 36 = 72°

Q6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Let one angle be x so another angle will also be x as they are adjacent angle.

so, x + x = 180°( adjacent angles of parallelogram are supplementary )

2x = 180°

x = \(\displaystyle \frac{{180{}^\circ }}{2}\)

x = 90°

so, the measure of each angle of parallelogram is 90°.

Q7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

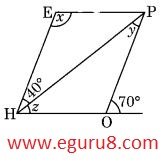
Solution:

∠1 + 70° = 180° ( Linear pair)

∠1 = 180° - 70°

∠1 = 110°

∠1 = ∠x ( opposite angles of parallelogram are equal)

∠x = 110°

∠y = 40° ( alternate angles of parallelogram are equal)

40° + z = 70° ( corresponding angles)

z = 70° - 40°

z =30°

Q8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

Solution:

i) In a parallelogram, opposite sides are equal.

so, 3x = 18

x = \(\displaystyle \frac{{18}}{3}\)

x = 6

Similarly

3y - 1 = 26

3y = 26 + 1

3y = 27

y = \(\displaystyle \frac{{27}}{3}\)

y = 9

ii)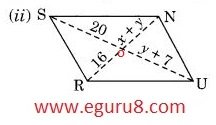

In parallelogram, the diagonals bisect each other. So according to this, OU=OS and RO = ON.

y+ 7 = 20

y = 20 - 7

y = 13

x+ y = 16

x + 13 = 16

x = 16 - 13

x = 3

So, the value of x is 3cm and the value of y is 13cm.

Q9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.

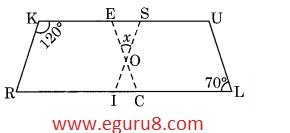
Solution:

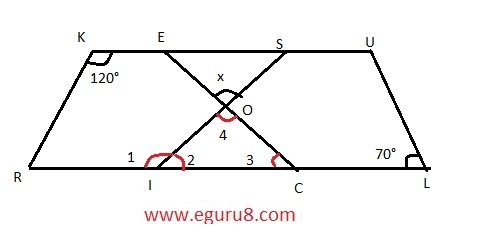
In parallelogram KRIS,

120° = ∠1 ( opposite angles of a parallelogram is equal)

∠1 = ∠2 = 180° ( Linear pair)

∠2 = 180° - 120°

∠2 = 60°

∠3 = 70° ( corresponding angles)

In ΔIOC

∠2 + ∠3 + ∠4 = 180° ( Angle sum property of triangle)

60° + 70° + ∠4 = 180°

130° + ∠4 = 180°

∠4 = 180° - 130°

∠4 = 50°

∠x = ∠4 ( vertically opposite angles)

∠x = 50°

So, the value of x is 50°.

Q10. Explain how this figure is a trapezium. Which of its two sides are parallel?

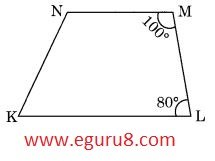
Solution: In this figure, ∠M and ∠L are acting as transversal. So, if we add ∠M and ∠L then,

∠M + ∠L

100º + 80º

= 180º

so we observe that measure of transversal line is 180º, so we can say that NM is parallel to KL and hence it proves that this figure is trapezium as it has parallel lines.

Q11. Find m∠C in figure 3.33 if \(\displaystyle \overline{{AB\,}}\parallel \,\overline{{DC}}\) .

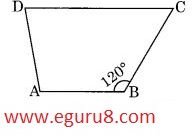
Solution: It is given that \(\displaystyle \overline{{AB\,}}\parallel \,\overline{{DC}}\). The angles formed by transverse lines measures 180º.

∠B + ∠C = 180º

120º + ∠C = 180º

∠C = 180º- 120º

∠C = 60º

Q12. Find the measure of ∠P and ∠S if \(\displaystyle \overline{{SP\,}}\parallel \,\overline{{RQ}}\) in Fig 3.34.( If you find m∠R, is there more than one method to find m∠P ?)

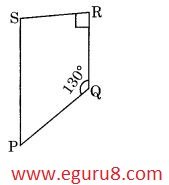
Solution: ∠P + ∠Q = 180º (sum of co- interior angle)

∠P + 130º = 180º

∠P = 180º - 130º

∠P = 50º

∠P + ∠Q + ∠R + ∠S = 360º (Angle sum property)

50º + 130º + 90º + ∠S = 360º

270º + ∠S = 360º

∠S = 360º - 270º

∠S = 90º

Yes, there are more than one method to find m∠P

\(\displaystyle \overline{{SP\,}}\parallel \,\overline{{RQ}}\)

∠S + ∠R = 180º

∠S + 90º = 180º

∠S = 90º

As we know that the sum of quadrilateral is 360º. So,

∠P + ∠Q + ∠R + ∠S = 360º (Angle sum property)

∠P + 130º + 90º + 90º = 360º

310º + ∠P = 360º

∠P = 360º - 310º

∠P = 50º

NCERT Class 8 Maths Chapter 3 Understanding Quadrilaterals :

NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3

Introduction

NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3

Leave a Comment Cancel Reply