NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2
Introduction
In chapter 3 Understanding Quadrilaterals Exercise 3.2, you will come to know about different types of polygons. a polygon is a plane figure enclosed by the line segment called sides. there are different types of polygon namely according to the number of line segments that is triangle which have three sides, while quadrilateral has four sides and pentagon has five sides and so on.
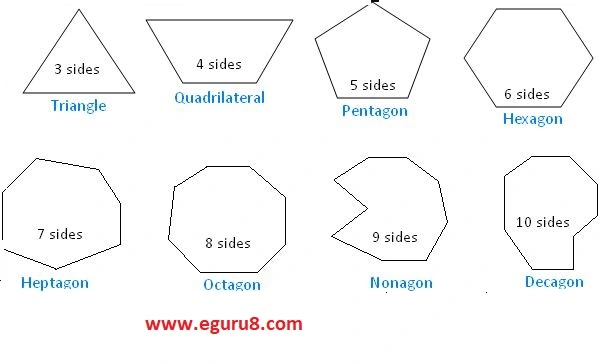
NCERT Class 8 Maths Chapter 3 Understanding Quadrilaterals :
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.1
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.4
NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2
Q1. Find x in the following figures.
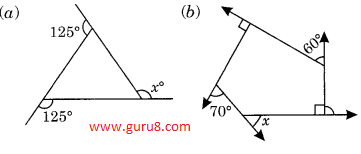
Solution:
a) ∠125° +∠125°+∠x = 360° (sum of all exterior angle is 360°)
∠250°+∠x = 360°
∠x = 360° - ∠250°
∠x = 110°
b) ∠90° + ∠ 70° + ∠x + ∠90° + ∠60° = 360° (sum of all exterior angle is 360°)
∠160° + ∠x + ∠150° = 360°
∠310° + ∠x = 360°
∠x = 360° - 310°
∠x = 50°
Q2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Solution:
i) measure of each exterior angle = \(\displaystyle \frac{{sum\,of\,all\,exterior\,angles}}{{No.\,of\,side}}\)
=\(\displaystyle \frac{{360{}^\circ }}{9}\)
= 40°
ii) measure of each exterior angle = \(\displaystyle \frac{{sum\,of\,all\,exterior\,angles}}{{No.\,of\,side}}\)
= \(\displaystyle \frac{{360{}^\circ }}{{15}}\)
= 24°
Q3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution: No. of sides = \(\displaystyle \frac{{Sum\,of\,all\,exterior\,angle}}{{measure\,of\,angle}}\)
=\(\displaystyle \frac{{360{}^\circ }}{{24{}^\circ }}\)
= 15 sides
Q4. How many sides does a regular polygon have if each of its interior angles is 165°?
Solution: Exterior angle = 180° - 165° = 15°
so,
No. of sides = \(\displaystyle \frac{{Sum\,of\,all\,exterior\,angle}}{{measure\,of\,angle}}\)
=\(\displaystyle \frac{{360{}^\circ }}{{15{}^\circ }}\)
= 24sides
Q5. (a) Is it possible to have a regular polygon with measure of each exterior angle a is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Solution:
a) No. of sides = \(\displaystyle \frac{{Sum\,of\,all\,exterior\,angle}}{{measure\,of\,angle}}\)
= \(\displaystyle \frac{{360{}^\circ }}{{22{}^\circ }}\)
=\(\displaystyle \frac{{180}}{{11}}\)
As, if we solve further, then answer will be in fraction and side can't be in fraction so, it is not possible to have a regular polygon with measure of each exterior angle as 22°.
b) Exterior angle = 180° - 22° (linear pair)
= 158°
No. of sides = \(\displaystyle \frac{{Sum\,of\,all\,exterior\,angle}}{{measure\,of\,angle}}\)
= \(\displaystyle \frac{{360{}^\circ }}{{158{}^\circ }}\)
= \(\displaystyle \frac{{180}}{{79}}\)
As, if we solve further, then answer will be in fraction and side can't be in fraction so, it is not possible to have a regular polygon with measure of each interior angle as 22°.
Q6. (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution:
a) The minimum interior angle possible for a regular polygon is 60° because equilateral triangle is the only regular polygon with minimum interior angle and its each angle is 60°.
b) The maximum exterior angle possible for a regular polygon is 120° (180°- 60° = 120°)
NCERT Class 8 Maths Chapter 3 Understanding Quadrilaterals :
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.1
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3
- Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.4