NCERT Solutions Of Class 8 Maths Chapter 5 Data Handling
Class 8 Maths Exercise 5.2 (Page-82)
Introduction
In this exercise we will come to know about circle graph. A circle graph shows the relationship between a whole and its parts. The whole circle is divided into sectors. The size of each sector is proportional to the activity or information it represents.
A circle graph is also called a Pie Chart.
Q1. A survey was made to find the type of music that a certain group of young people liked in a city. The adjoining pie chart shows the findings of this survey.
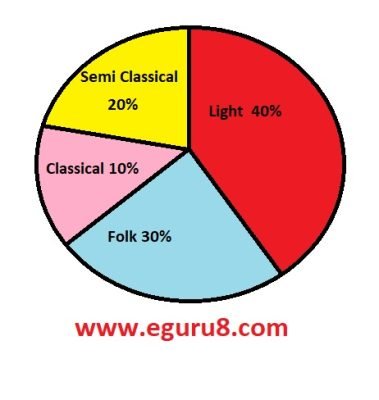
From this pie chart answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CDs. How many of each type would they make?
Solution:
i) Let total number of young people be x
So, 10% of x = 20
then, \(\displaystyle \frac{{10x}}{{100}}\) \(\displaystyle \times \) = 20
10x = 20 \(\displaystyle \times \) 100
10x = 2000
x = \(\displaystyle \frac{{2000}}{{10}}\)
x = 200
so, if 20 people liked classical music, then 200 young people were surveyed.
ii) Light music is liked by the maximum number of people.
iii) Classical= \(\displaystyle \frac{{10}}{{100}}\times 1000\)
= 10 \(\displaystyle \times \) 10
= 100CD's
Semi Classical = \(\displaystyle \frac{{20}}{{100}}\times 1000\)
= 20 \(\displaystyle \times \) 10
= 200 CD's
Folk = \(\displaystyle \frac{{30}}{{100}}\times 1000\)
= 30 \(\displaystyle \times \) 10
= 300 CD's
Light = \(\displaystyle \frac{{40}}{{100}}\times 1000\)
= 40 \(\displaystyle \times \) 10
= 400 CD's
Q2. A group of 360 people were asked to vote for their favorite season from the three seasons rainy, winter and summer.
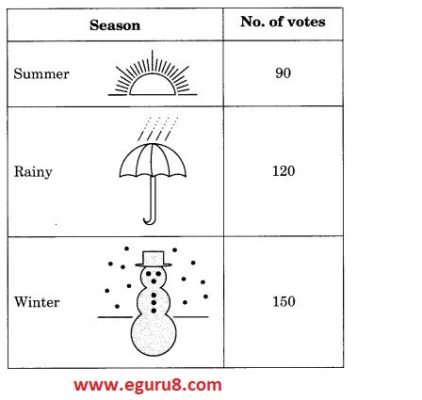
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.
Solution:
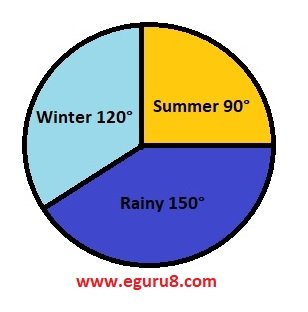
i) Winter season got the most votes.
ii) Summer = \(\displaystyle \frac{{90}}{{360}}\times 360\)
= 90°
Rainy = \(\displaystyle \frac{{120}}{{360}}\times 360\)
= 120°
Winter = \(\displaystyle \frac{{150}}{{360}}\times 360\)
= 150°
iii)
Q3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
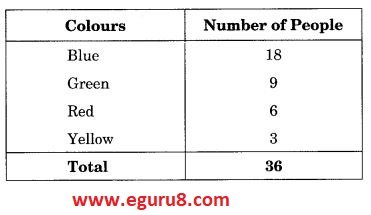
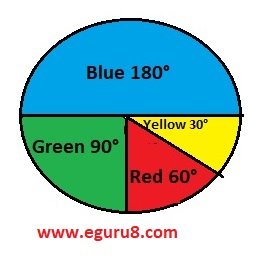
Solution: For pie chart we have to find the central angle of each colour.
Central angle of Blue =\(\displaystyle \frac{{18}}{{36}}\times 360{}^\circ \,=180{}^\circ \)
Central angle of Green = \(\displaystyle \frac{{9}}{{36}}\times 360{}^\circ \,=90{}^\circ \)
Central angle of Red = \(\displaystyle \frac{{6}}{{36}}\times 360{}^\circ \,=60{}^\circ \)
Central angle of Yellow = \(\displaystyle \frac{{3}}{{36}}\times 360{}^\circ \,=30{}^\circ \)
Q4. The following pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
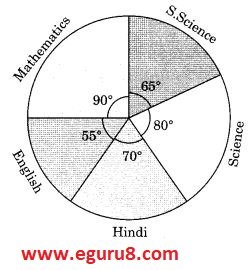
(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi. (Hint: Just study the central angles).
Solution: To find out marks we will multiply the given angle and divide it with 360.
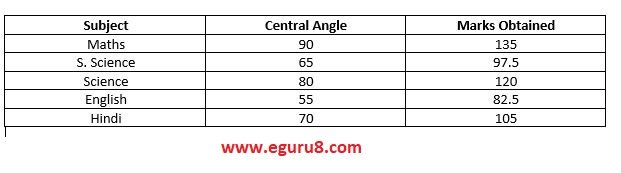
i) In Hindi the student scored 105 marks.
ii) 135 - 105 = 30.
So, 30 more marks were obtained by student in mathematics than in Hindi.
iii) Marks of S.science and mathematics = 97.5 + 135 = 232.5
Marks of Science and Hindi = 120 + 105 = 225
Yes,the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
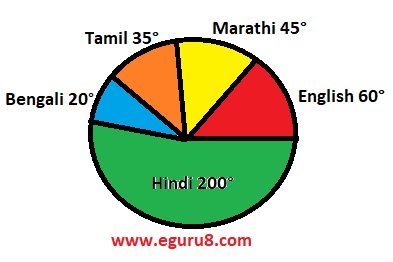
Q5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.
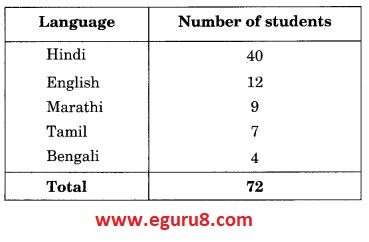
Solution: Central angle of Hindi = \(\displaystyle \frac{{40}}{{72}}\times 360{}^\circ \) = 200°
Central angle of English = \(\displaystyle \frac{{12}}{{72}}\times 360{}^\circ \) = 60°
Central angle of Marathi = \(\displaystyle \frac{{9}}{{72}}\times 360{}^\circ \) = 45°
Central angle of Tamil = \(\displaystyle \frac{{7}}{{72}}\times 360{}^\circ \) = 35°
Central angle of Bengali = \(\displaystyle \frac{{4}}{{72}}\times 360{}^\circ \) = 20°