NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.4

Introduction:

In this exercise/article we will learn about multiplication of algebraic expressions. multiplying a polynomials by a polynomial and multiplying a binomials by a binomials and multiplying a binomials by a trinomials. Only on multiply do in this exercise. Most important thing bracket multiply bracket.

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

Class 8 Maths Exercise 9.4 (Page-148)

Q1. Multiply the binomials.

(i) ( 2x + 5 ) and ( 4x - 3 )

Solution :

We have to multiply the first bracket by the second bracket ( 2x + 5 ) × ( 4x - 3 )

= 2x ( 4x - 3 ) + 5 ( 4x - 3 )

= 8x² - 6x + 20x - 15

= 8x² + 14x - 15

So, answer is 8x² + 14x - 15

(ii) ( y - 8 ) and ( 3y - 4 )

Solution :

We have to multiply the first bracket by the second bracket ( y - 8 ) × ( 3y - 4 )

= y ( 3y - 4 ) - 8 ( 3y - 4 )

= 3y² - 4y - 24y + 32

= 3y² - 28y + 32

So, answer is 3y² - 28y + 32

(iii) ( 2.5l - 0.5m ) and ( 2.5l + 0.5m )

Solution :

We have to multiply the first bracket by the second bracket ( 2.5l - 0.5 m ) × ( 2.5l + 0.5m )

= 2.5l ( 2.5l + 0.5m ) - 0.5m ( 2.5l + 0.5m )

= 6.25l² + 1.25lm - 1.25lm - 0.25m²

= 6.25l² - 0.25m²

So, answer is 6.25l² + 1.25lm - 1.25lm - 0.25m²

(iv) ( a + 3b ) and ( x + 5 )

Solution :

We have to multiply the first bracket by the second bracket ( a + 3b ) × ( x + 5 )

= a ( x + 5 ) + 3b ( x + 5 )

= ax + 5a + 3bx + 15b

So, answer is ax + 5a + 3bx + 15b

(v) ( 2pq + 3q² ) and ( 3pq - 2q² )

Solution :

We have to multiply the first bracket by the second bracket ( 2pq + 3q² ) × ( 3pq - 2q² )

= 2pq ( 3pq - 2q² ) + 3q² ( 3pq - 2q² )

= 6p²q² - 4pq³ + 9pq³ - 6q⁴

= 6p²q² + 5pq³ - 6q⁴

So, answer is 6p²q² + 5pq³ - 6q⁴

(vi) \(\displaystyle \left( {\frac{3}{4}{{a}^{2}}\,+\,3{{b}^{2}}} \right)\,and\,4\,\left( {{{a}^{2}}\,-\,\frac{2}{3}{{b}^{2}}} \right)\)

Solution :

We have to multiply the first bracket by the second bracket\(\displaystyle \left( {\frac{3}{4}{{a}^{2}}\,+\,3{{b}^{2}}} \right)\,\times \,4\,\left( {{{a}^{2}}\,-\,\frac{2}{3}{{b}^{2}}} \right)\)

= \(\displaystyle \left( {\frac{3}{4}{{a}^{2}}\,+\,3{{b}^{2}}} \right)\,\times \,\left( {4{{a}^{2}}\,-\,\frac{8}{3}{{b}^{2}}} \right)\)

= \(\displaystyle \frac{3}{4}{{a}^{2}}\left( {4{{a}^{2}}-\frac{8}{3}{{b}^{2}}} \right)+3{{b}^{2}}\left( {4{{a}^{2}}-\frac{8}{3}{{b}^{2}}} \right)\)

\(\displaystyle =\,\left( {\frac{3}{4}{{a}^{2}}\times 4{{a}^{2}}-\frac{3}{4}{{a}^{2}}\times \frac{8}{3}{{b}^{2}}} \right)\,\,+\,\left( {3{{b}^{2}}\times 4{{a}^{2}}-3{{b}^{2}}\times \frac{8}{3}{{b}^{2}}} \right)\)

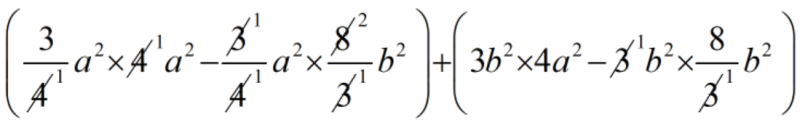
= \(\displaystyle 3{{a}^{4}}\,-\,2{{a}^{2}}{{b}^{2}}\,+\,12{{a}^{2}}{{b}^{2}}\,-\,8{{b}^{4}}\)

= \(\displaystyle 3{{a}^{4}}\,+\,10{{a}^{2}}{{b}^{2}}\,-\,8{{b}^{4}}\)

So, answer is \(\displaystyle 3{{a}^{4}}\,+\,10{{a}^{2}}{{b}^{2}}\,-\,8{{b}^{4}}\)

Q2. Find the product.

(i) ( 5 - 2x ) ( 3 + x )

Solution :

We have to multiply the first bracket by the second bracket ( 5 - 2x ) × ( 3 + x )

= 5 ( 3 + x ) - 2x ( 3 + x )

= 15 + 5x - 6x - 2x²

= 15 - x - 2x²

So, answer is 15 - x - 2x²

(ii) ( x + 7y ) ( 7x - y )

Solution :

We have to multiply the first bracket by the second bracket ( x + 7y ) × ( 7x - y )

= x ( 7x - y ) + 7y ( 7x - y )

= 7x² - xy + 49xy - 7y²

= 7x² + 48xy - 7y²

So, answer is 7x² + 48xy - 7y²

(iii) ( a² + b ) ( a + b² )

Solution :

We have to multiply the first bracket by the second bracket ( a² + b ) × ( a + b² )

= a² ( a + b² ) + b ( a + b² )

= a³ + a² b² + ab + b³

So, answer is a³ + a² b² + ab + b³

(iv) ( p² - q² ) ( 2p + q )

Solution :

We have to multiply the first bracket by the second bracket ( p² - q² ) × ( 2p + q )

= p² ( 2p + q ) - q² ( 2p + q )

= 2p³ + p²q - 2pq² - q³

So, answer is 2p³ + p²q - 2pq² - q³

Class 8 Maths Chapter 9 Exercise 9.4

Q3. Simplify.

(i) ( x² - 5 ) ( x + 5 ) + 25

Solution :

We have to multiply the first bracket by the second bracket ( x² - 5 ) ( x + 5 ) + 25

= x² ( x + 5 ) - 5 ( x + 5 ) + 25

= x³ + 5x² - 5x - 25 + 25 [ because, 25 - 25 = 0 ]

= x³ + 5x² - 5x

So, answer is x³ + 5x² - 5x

(ii) ( a² + 5 ) ( b³ + 3 ) + 5

Solution :

We have to multiply the first bracket by the second bracket ( a² + 5 ) ( b³ + 3 ) + 5

= a² ( b³ + 3 ) + 5 ( b³ + 3 ) + 5

= a²b³ + 3a² + 5b³ + 15 + 5 [ because, 15 + 5 = 20 ]

= a²b³ + 3a² + 5b³ + 20

So, answer is a²b³ + 3a² + 5b³ + 20

(iii) ( t + s² ) ( t² - s )

Solution :

We have to multiply the first bracket by the second bracket ( t + s² ) ( t² - s )

= t ( t² - s ) + s² ( t² - s )

= t³ - st + s²t² - s³

So, answer is t³ - st + s²t² - s³

(iv) ( a + b ) ( c - d ) + ( a - b ) ( c + d ) + 2( ac + bd )

Solution :

We have to multiply the first bracket by the second bracket ( a + b ) ( c - d ) + ( a - b ) ( c + d ) + 2( ac + bd )

= a ( c - d ) + b ( c - d ) + a ( c + d ) - b ( c + d ) + 2ac + 2bd

= ac - ad + bc - bd + ac + ad - bc - bd + 2ac + 2bd

= ( ac + ac ) ( - ad + ad ) ( bc - bc ) ( - bd - bd ) + 2ac + 2bd [ because - ad + ad = 0 , bc - bc = 0 ]

= ( 2ac + 2ac ) ( - 2bd + 2bd ) [ because - 2bd + 2bd = 0 ]

= 4ac

So, answer is 4ac

(v) ( x + y ) ( 2x + y ) + ( x + 2y ) ( x - y )

Solution :

We have to multiply the first bracket by the second bracket ( x + y ) ( 2x + y ) + ( x + 2y ) ( x - y )

= x ( 2x + y ) + y ( 2x + y ) + x ( x - y ) + 2y ( x - y )

= 2x² + xy + 2xy + y² + x² - xy + 2xy - 2y²

= ( 2x² + x² ) ( 2xy + 2xy ) ( - 2y² + y² ) ( xy - xy ) [ because, xy - xy = 0 ]

= 3x² + 4xy - y²

So, answer is 3x² + 4xy - y²

(vi) ( x + y ) ( x² - xy + y² )

solution :

We have to multiply the first bracket by the second bracket ( x + y ) ( x² - xy + y² )

= x ( x² - xy + y² ) + y ( x² - xy + y² )

= x³ - x²y + xy² + x²y - xy² + y³

= x³ + y³ ( - x²y + x²y ) ( xy² - x²y ) [ because, - x²y + x²y = 0 , xy² - x²y = 0 ]

= x³ + y³

= So, answer is x³ + y³

(vii) ( 1.5x - 4y ) ( 1.5x + 4y + 3 ) - 4.5x + 12y

Solution :

We have to multiply the first bracket by the second bracket ( 1.5x - 4y ) ( 1.5x + 4y + 3 ) - 4.5x + 12y

= 1.5x ( 1.5x + 4y + 3 ) - 4y ( 1.5x + 4y + 3 ) - 4.5x + 12y

= 2.25x² + 6xy + 4.5x - 6xy - 16y² - 12y - 4.5x + 12y

= 2.25x² - 16y² ( 6xy - 6xy ) ( 4.5x - 4.5x ) ( - 12y + 12y ) [ because, 6xy - 6xy = 0 , 4.5x - 4.5x = 0 , - 12y + 12y = 0 ]

= 2.25x² - 16y²

= So, answer is 2.25x² - 16y²

(viii) ( a + b + c ) ( a + b - c )

Solution :

We have to multiply the first bracket by the second bracket ( a + b + c ) ( a + b - c )

= a ( a + b - c ) + b ( a + b - c ) + c ( a + b - c )

= a² + ab - ac + ab + b² - bc + ac + bc - c²

= a² + b² - c² + ( ab + ab ) ( - ac + ac ) ( - bc + bc ) [ because, - ac + ac = 0 , - bc + bc = 0 ]

= a² + b² - c² + 2ab

So, answer is a² + b² - c² + 2ab .

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :

NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.4

Introduction:

Class 8 Maths Exercise 9.4 (Page-148)

Class 8 Maths Chapter 9 Exercise 9.4

Leave a Comment Cancel Reply