NCERT Solutions Class 8 Maths Chapter 11 Mensuration Exercise 11.3
Introduction :
In this exercise we will come to know about Mensuration. Solid shapes like Soap, toy, pastes and snacks etc. Surface area of cube, cuboid and cylinder. Right circular cylinders.
NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry :
- Class 8 Maths Chapter 11 Mensuration Exercise 11.1
- Class 8 Maths Chapter 11 Mensuration Exercise 11.2
- Class 8 Maths Chapter 11 Mensuration Exercise 11.3
- Class 8 Maths Chapter 11 Mensuration Exercise 11.4
Class 8 Maths Mensuration Exercise-11.3
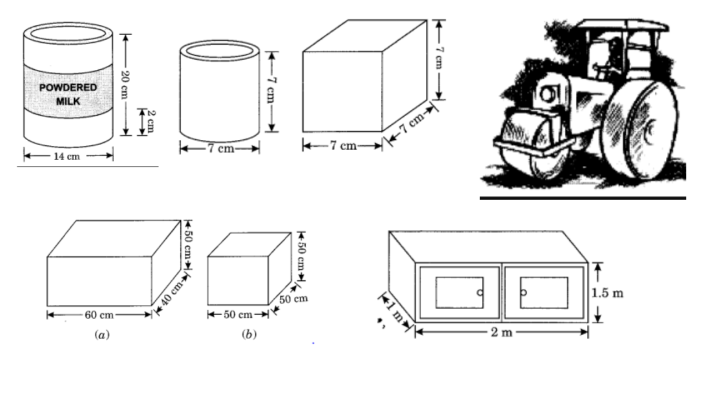
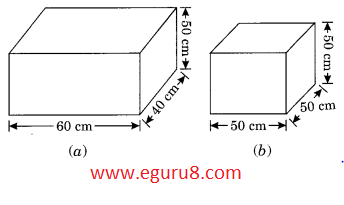
Q1. There are two cuboidal boxes as shown in the figure. Which box requires the lesser amount of material to make?
Solution:
Given:
dimension of first cuboidal box = 60cm × 40cm × 50cm
dimension of second cuboidal box = 50cm × 50cm × 50cm
As, to find the material required we fill find the total surface area of both figure
so,
Total surface area of cuboid = 2(lb + bh + hl)
= 2(60×40 + 40×50 + 50×60)
= 2(2400 + 2000 + 3000)
= 2 × 7400
= 14800cm2
As in the second figure all sides are same, so we can say that it is a cube
so,
Total surface area of cube = 6l2
= 6(50)2
= 6(50 × 50)
= 6 × 2500
= 15000cm2
so, the first figure(a) will requires lesser amount of material to make.
Q2. A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width 96 cm is required to cover 100 such suitcases.
Solution:
Given: length of suitcase = 80cm
breadth of suitcase = 48cm
height of suitcase = 24 cm
width of tarpaulin = 96cm
\(\displaystyle \begin{array}{l}Total\,surface\,area\,of\,suitcase\,=\,2(lb+bh+hl)\\=\,2\,(80\times 48+48\times 24+24\times 80)\\=2(3840+1152+1920)\\=2\times 6912\\=13824c{{m}^{2}}\\Area\,of\,100\,suitcase\,=\,100\,\times \,13824c{{m}^{2}}\\=\,1382400c{{m}^{2}}\\\end{array}\)
As,the tarpaulin is in rectangular shape so the area of tarpaulin is = length \(\displaystyle \times \) breadth
=l \(\displaystyle \times \) 96
=96l \(\displaystyle c{{m}^{2}}\)
Area of 100 suitcase is equal to area of tarpaulin
so,
Area of 100 suitcase = Area of tarpaulin
1382400 = 96l
\(\displaystyle \begin{array}{l}l=\,\frac{{1382400}}{{96}}\\l=14400cm\end{array}\)
= 144m(convert from cm to m)
hence, 144m tarpaulin is required to cover 100 suitcase.
Q3. Find the side of a cube whose surface area is 600 cm\(\displaystyle ^{2}\).
Solution:
\(\displaystyle \begin{array}{l}Surface\,area\,of\,cube\,=\,6{{l}^{2}}\\600\,=\,6{{l}^{2}}\\{{l}^{2}}=\,\frac{{600}}{6}\\{{l}^{2}}\,=\,100\\l\,=\,\sqrt{{100}}\\l\,=\,10cm\end{array}\)
So, the side of a cube is 10cm.
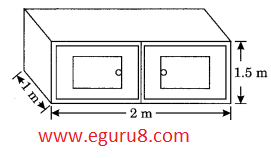
Q4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
Solution:
Given: length of cabinet= 2m
breadth of cabinet = 1m
height of cabinet = 1.5m
According to question, we will subtract the area of bottom part from the remaining surface of cabinet.
\(\displaystyle \begin{array}{l}=Area\,of\,cabinet\,-\,Area\,of\,bottom\\=\,2(lb+bh+hl)-\,lb\\=\,2(2\times 1+1\times 1.5+1.5\times 2)-2\times 1\\=\,2(2+1.5+3)-2\\=\,2\,(6.5)-2\\=\,13-2\\=\,11{{m}^{2}}\end{array}\)
so, Rukshar will cover \(\displaystyle 11{{m}^{2}}\) area if she painted all except the bottom of the cabinet.
Q5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m of the area is painted. How many cans of paint will she need to paint the room?
Solution:
Given: length of cuboidal hall = 15m
Breadth of cuboidal hall = 10m
height of cuboidal hall = 7m
Area of can = 100\(\displaystyle {{m}^{2}}\)
According to the question we have to subtract the base of hall from the area of hall
\(\displaystyle \begin{array}{l}=Area\,of\,hall\,-\,Area\,of\,base\\=\,2(lb+bh+hl)-\,lb\\=\,2(15\times 10+10\times 7+7\times 15)-15\times 10\\=\,2(150+70+105)-150\\=\,2\,(325)-150\\=\,650-150\\=\,500{{m}^{2}}\end{array}\)
\(\displaystyle Number\,of\,can\,=\frac{{Area\,of\,hall}}{\begin{array}{l}area\,of\,can\\=\frac{{500}}{{100}}\\=\,5\,cans\end{array}}\)
Hence, she need 5 cans to paint the hall.
Q6. Describe how the two figures at the right are alike and how they are different. Which box has a larger lateral surface area?

Solution: the two figures are alike as their dimensions are same and their shapes are different, one is cylindrical an the other one is cube in shape.
Lateral surface area of cylinder = \(\displaystyle 2\pi rh\)
\(\displaystyle \begin{array}{l}2\times \frac{{22}}{7}\times \,3.5\,\times \,7\\=2\times 22\times 3.5\\=44\times \,3.5\\=\,154c{{m}^{2}}\end{array}\)
Lateral surface area of cube = 4\(\displaystyle {{a}^{2}}\)
\(\displaystyle \begin{array}{l}=\,4{{a}^{2}}\\=\,4\,\times {{(7)}^{2}}\\=\,4\times 49\\=\,196c{{m}^{2}}\end{array}\)
From the above observation, cube has the larger lateral surface area.
Q7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How many sheets of metal is required?
Solution:
Given: radius of tank = 7m
Height of tank = 3m
Total surface area of cylinder tank = \(\displaystyle 2\pi r(r+h)\)
\(\displaystyle \begin{array}{l}=\,2\pi r(r+h)\\=\,2\times \frac{{22}}{7}\times 7(7+3)\\=\,2\times \frac{{22}}{7}\times 7(10)\\=\,2\times 22\times (10)\\=\,44\times 10\\=\,440{{m}^{2}}\end{array}\)
Hence, 440\(\displaystyle {{m}^{2}}\) sheet of metal is required.
Q8. The lateral surface area of a hollow cylinder is 4224\(\displaystyle c{{m}^{2}}\) . It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of the rectangular sheet.
Solution:
Given: area of hollow cylinder = 4224\(\displaystyle c{{m}^{2}}\)
width of rectangle = 33cm
Lateral surface area of cylinder = area of rectangular sheet
4224 = l\(\displaystyle \times \) b
4224 = l \(\displaystyle \times \) 33
l = \(\displaystyle \frac{{4224}}{{33}}\)
l = 128cm
Now,
Perimeter of Rectangle = 2 \(\displaystyle \times \)(l+b)
= 2 \(\displaystyle \times \) (128+33)
=2\(\displaystyle \times \)(161)
= 322cm
hence, the perimeter of rectangular sheet is 322cm.
Q9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.

Solution:
Given: Diameter of road roller= 84cm
length of road roller = 1m
Lateral surface area of road roller = \(\displaystyle 2\pi rh\)
\(\displaystyle \begin{array}{l}=\,2\,\times \frac{{22}}{7}\times 42\times 100\,(r=\frac{d}{2})(convert\,m\,to\,cm)\\=2\times \,22\,\times 6\,\times 100\\=\,44\times 600\\=\,26400c{{m}^{2}}\end{array}\)
Area covered by road roller in 750 revolutions = 26400 \(\displaystyle \times \) 750
=19800000 \(\displaystyle c{{m}^{2}}\)
hence, the area of road is 1980 \(\displaystyle {{m}^{2}}\) . (convert \(\displaystyle c{{m}^{2}}\) to \(\displaystyle {{m}^{2}}\))
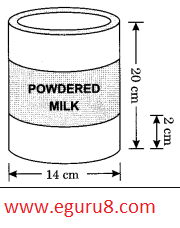
Q10. A company packages its milk powder in a cylindrical container whose base has a diameter of 14 cm and height 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?
Solution:
Given: diameter of container = 14cm
height of container = 20cm
Diameter of label = 14cm
height of label= 20-4 = 16cm
Area of label = \(\displaystyle 2\pi rh\)
\(\displaystyle \begin{array}{l}=\,2\times \frac{{22}}{7}\times 7\times 16\,(r=\frac{d}{2})\\=\,2\times 22\times 16\\=\,44\times 16\\=\,704c{{m}^{2}}\end{array}\)
hence, the area of the label is 704\(\displaystyle c{{m}^{2}}\).
NCERT Class 9 Maths Chapter 5 Introduction to Euclid's Geometry :
