NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.3
Introduction:
In this exercise/article we will learn about multiplication of algebraic expressions. multiplying a monomials by a polynomial and multiplying a monomials by a binomial and multiplying a monomials by a trinomial and multiply or add and subtract then do this exercise.
NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.1
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.2
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.3
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.4
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.5
Class 8 Maths Exercise 9.3 (Page-146)
Q1. Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p , q + r
Solution :
we have 4p , q + r
we know very well
So, 4p(q + r )
= 4pq + 4pr
(ii) ab , a - b
Solution :
We have ab , a - b
we know very well
So, ab( a - b )
= a2b - ab2
(iii) a + b , 7a2b2
Solution :
We have a + b , 7a2b2
we know very well
So, ( a + b ) ( 7a2b2 )
= 7a3b2 + 7a2b3
(iv) a2 - 9 , 4a
Solution :
We have a2 - 9 , 4a
we know very well
So, 4a( a2 - 9 )
= 4a3 - 36a
(v) pq + qr + rp , 0
Solution :
We have pq + qr + rp , 0
we know very well
= 0( pq + qr + rp )
= o + o + o
= o
Q2. Complete the table

Solution :
Multiply the first expression by the second expression

= a ( b + c + d ) = ( a × b ) + ( a × c ) + ( a × d ) = ab + ac + ad
= 5xy ( x + y - 5 ) = ( 5xy × x ) + ( 5xy × y ) - ( 5xy × 5 ) = 5x2y + 5xy2 - 25xy
= p ( 6p2 - 7p + 5 ) = ( p × 6p2 ) - ( p × 7p ) + ( p × 5 ) = 6p3 - 7p2 + 5p
= 4p2q2 ( p2 - q2 ) = ( 4p2q2 × p2 ) - ( 4p2q2 × q2 ) = 4p4q2 - 4p2q4
= abc ( a + b + c ) = ( abc × a ) + ( abc × b ) + ( abc × c ) = a2bc + ab2c + abc2
Class 8 Maths Chapter 9 Exercise 9.3
Q3. find the product
(i) ( a2 ) × ( 2a22 ) × ( 4a26 )
Solution :
We have ( a2 ) × ( 2a22 ) × ( 4a26 )
= 2 × 4 × a( 2 + 22 + 26 )
= 8a( 50 )
= 8a50
(ii) \(\displaystyle \left[ {\frac{2}{3}xy} \right]\times \left[ {\frac{{-9}}{{10}}{{x}^{2}}{{y}^{2}}} \right]\)
Solution :
We have \(\displaystyle \left[ {\frac{2}{3}xy} \right]\times \left[ {\frac{{-9}}{{10}}{{x}^{2}}{{y}^{2}}} \right]\)
![]()
= \(\displaystyle \,\frac{{-3}}{5}\times {{x}^{3}}\times {{y}^{3}}\)
= \(\displaystyle \frac{{-3}}{5}{{x}^{3}}{{y}^{3}}\)
(iii) \(\displaystyle \left[ {-\frac{{10}}{3}p{{q}^{3}}} \right]\times \left[ {\frac{6}{5}{{p}^{3}}q} \right]\)
Solution :
We have \(\displaystyle \left[ {-\frac{{10}}{3}p{{q}^{3}}} \right]\times \left[ {\frac{6}{5}{{p}^{3}}q} \right]\)
![]()
= \(\displaystyle -\,\frac{4}{1}\,\times \,{{p}^{4}}\,\times \,{{q}^{4}}\)
= \(\displaystyle -\,4{{p}^{4}}{{q}^{4}}\)
(iv) \(\displaystyle x\,\times \,{{x}^{2}}\,\times \,{{x}^{3}}\,\times \,{{x}^{4}}\)
Solution :
we have \(\displaystyle x\,\times \,{{x}^{2}}\,\times \,{{x}^{3}}\,\times \,{{x}^{4}}\)
= \(\displaystyle x{{\,}^{{(\,1\,+\,2\,+\,3\,+\,4\,)}}}\)
= \(\displaystyle x{{\,}^{{(\,10\,)}}}\)
= \(\displaystyle x{{\,}^{{10}}}\)
Q4. (a) Simplify 3x ( 4x - 5 ) + 3 and find its values for (i) x = 3 , (ii) x = \(\displaystyle \frac{1}{2}\)
Solution :
(i) We have 3x ( 4x - 5 ) + 3
= 12x2 - 15x + 3
= Now , put x = 3
= 12( 3 )2 - 15 × 3 + 3
= 12( 9 ) - 45 + 3
= 108 - 45 + 3
= 111 - 45
= 66
(ii) We have 3x ( 4x - 5 ) + 3
= 12x2 - 15x + 3
= Now, put x = \(\displaystyle \frac{1}{2}\)
= \(\displaystyle 12{{\left[ {\frac{1}{2}} \right]}^{2}}-\,15\,\times \,\frac{1}{2}\,+\,3\)
= \(\displaystyle 12\,\times \,\frac{1}{4}\,-\,\frac{{15}}{2}\,+\,3\)
= 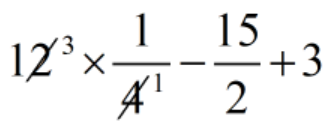
= \(\displaystyle 3\,-\,\frac{{15}}{2}\,+\,3\)
= \(\displaystyle 6\,-\,\frac{{15}}{2}\)
= \(\displaystyle \frac{{12\,-\,15}}{2}\)
= \(\displaystyle \frac{{-3}}{2}\)
(b) Simplify a ( a2 + a + 1 ) + 5 and find its values for (i) a = 0 , (ii) a = 1
Solution :
We have a ( a2 + a + 1 ) + 5
= a3 + a2 + 1a + 5
= Now, put x = 0
= 03 + 02 + 1 × 0 + 5
= 0 + 0 + 0 + 5
= 5
(ii) We have a ( a2 + a + 1 ) + 5
= a3 + a2 + 1a + 5
= Now, put x = 1
= 13 + 12 + 1 × 1 + 5
= 1 + 1 + 1 + 5
= 8
Q5. (a) Add : p ( p - q ) , q ( q - r ) and r ( r - p )
Solution :
We have p ( p - q ) , q ( q - r ) and r ( r - p )
So, add all these
p ( p - q ) + q ( q - r ) + r ( r - p )
= p2 - pq + q2 - qr + r2 - rp
= p2+ q2 + r2- pq - qr - rp
(b) Add : 2x ( z - x - y ) and 2y ( z - y - x )
Solution :
We have 2x ( z - x - y ) and 2y ( z - y - x )
So, add all these
2x ( z - x - y ) + 2y ( z - y - x )
= 2zx - 2x2 - 2xy + 2yz - 2y2 - 2xy
= 2zx - 2x2 - 4xy + 2yz - 2y2
= - 2x2 - 2y2 - 4xy + 2yz + 2zx
(c) Subtract : 3l ( l - 4m + 5n ) from 4l ( 10n - 3m + 2l )
Solution :
We have 3l ( l - 4m + 5n ) from 4l ( 10n - 3m + 2l )
So, subtract all these
4l ( 10n - 3m + 2l ) - 3l ( l - 4m + 5n )
= 40ln - 12ml + 8l2 - 3l2 + 12ml - 15nl
= 40ln - 15nl - 12ml + 12ml + 8l2 - 3l2
= 25ln + 5l2
= 5l2 + 25ln
(d) Subtract : 3a ( a + b + c ) - 2b ( a - b + c ) from 4c ( -a + b + c )
Solution :
We have 3a ( a + b + c ) - 2b ( a - b + c ) from 4c ( -a + b + c )
So, subtract all these
4c ( -a + b + c ) - { 3a ( a + b + c ) - 2b ( a - b + c ) }
= 4c ( -a + b + c ) - 3a ( a + b + c ) + 2b ( a - b + c )
= - 4ac + 4bc + 4c2 - 3a2 - 3ab - 3ac + 2ab - 2b2 + 2bc
= ( -4ac - 3ac ) ( 4bc + 2bc ) ( - 3ab + 2ab ) ( 4c2 - 3a2 - 2b2 )
= ( -7ac ) ( 2bc ) ( -ab ) ( 4c2 - 3a2 - 2b2 )
= - 7ac + 6bc - ab + 4c2 - 3a2 - 2b2
= - 3a2 - 2b2 + 4c2 - ab + 6bc - 7ac .
NCERT Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities :
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.1
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.2
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.3
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.4
- NCERT Class 8 Maths Algebraic Expressions and Identities Exercise 9.5