NCERT Solutions Class 9 Maths Chapter 6 Lines And Angles
Introduction:
In this chapter we will learn about Lines And Angles. In Chapter 5, you have studied that a minimum of two points are required to draw a line. You have also studied some axioms and, with the help of these axioms, you
proved some other statements. In this chapter, you will study the properties of the
angles formed when two lines intersect each other, and also the properties of the angles formed when a line intersects two or more parallel lines at distinct points.
Further you will use these properties to prove some statements using deductive reasoning
(see Appendix 1). You have already verified these statements through some activities
in the earlier classes.
In this chapter, you have studied the following points:
1. If a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and viceversa. This property is called as the Linear pair axiom.
2. If two lines intersect each other, then the vertically opposite angles are equal.
3. Lines which are parallel to a given line are parallel to each other.
NCERT Class 9 Maths Chapter 6 Lines And Angles :
NCERT Solutions Class 9 Maths Chapter 6 Lines And Angles Exercise 6.1
In this exercise-6.1 we will learn about Lines And Angles. Recall that a part (or portion) of a line with two end points is called a line-segment and a part of a line with one end point is called a ray. Note that the line segment AB is denoted by \(\displaystyle \overline{{AB}}\) , and its length is denoted by AB. The ray AB is denoted by \(\displaystyle \overrightarrow{{AB}}\) , and a line is denoted by \(\displaystyle \overleftrightarrow{{AB}}\).
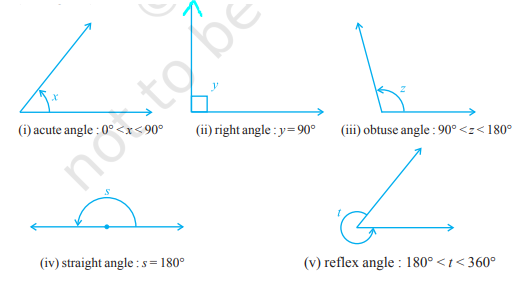
(i) An acute angle measures between 0\(\displaystyle ^{\circ }\) and 90\(\displaystyle ^{\circ }\)
(ii) A right angle is exactly equal to 90\(\displaystyle ^{\circ }\)
(iii) An angle greater than 90\(\displaystyle ^{\circ }\) but less than 180\(\displaystyle ^{\circ }\) is called an obtuse angle.
(iv) A striaght angle is equal to 180\(\displaystyle ^{\circ }\)
(v) An angle which is greater than 180\(\displaystyle ^{\circ }\) but less than 360\(\displaystyle ^{\circ }\) is called a reflex angle.
Further, two angles whose sum is 90\(\displaystyle ^{\circ }\) are called complementary angles, and two angles whose sum is 180\(\displaystyle ^{\circ }\) are called supplementary angles.
- Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms areon different sides of the common arm.
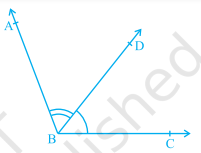
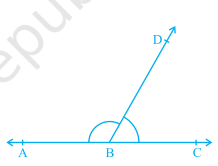
- If the non–common arms BA and BC in, form a line then it will look like. In this case, ∠ ABD and ∠ DBC are called linear pair of angles.
- You may also recall the vertically opposite angles formed when two lines, say AB and CD,
intersect each other, say at the point o.There are two pairs of vertically opposite angles.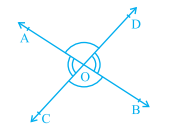
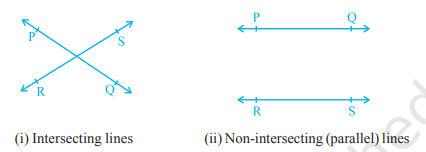
- Recall the notion of a line, that it extends indefinitely in both directions. Lines PQ and RS in (i) are intersecting lines and in (ii) are parallel lines. Note that the lengths of the common perpendiculars at different points on these parallel lines is the same. This equal length is called the distance between two parallel lines.
NCERT Solutions Class 9 Maths Chapter 6 Lines And Angles Exercise 6.2
In this exercise-6.2 we will learn about Lines And Angles. Lines parallel to the same line. Lines which are parallel to a given line are parallel to each other. Parallel lines and a transversal.
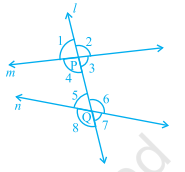
(a) Corresponding angles :
(i) ∠ 1 and ∠ 5 (ii) ∠ 2 and ∠ 6
(iii) ∠ 4 and ∠ 8 (iv) ∠ 3 and ∠ 7
(b) Alternate interior angles :
(i) ∠ 4 and ∠ 6 (ii) ∠ 3 and ∠ 5
(c) Alternate exterior angles:
(i) ∠ 1 and ∠ 7 (ii) ∠ 2 and ∠ 8
(d) Interior angles on the same side of the transversal:
(i) ∠ 4 and ∠ 5 (ii) ∠ 3 and ∠ 6.
- If a transversal intersects two parallel lines, then
(i) each pair of corresponding angles is equal,
(ii) each pair of alternate interior angles is equal,
(iii) each pair of interior angles on the same side of the transversal is supplementary.
- If a transversal intersects two lines such that, either
(i) any one pair of corresponding angles is equal, or
(ii) any one pair of alternate interior angles is equal, or
(iii) any one pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.
