NCERT Solutions Class 9 Maths Chapter 6 Lines And Angles Exercise 6.2
Introduction:
In this exercise/article we will learn about Lines And Angles. Lines parallel to the same line. Lines which are parallel to a given line are parallel to each other. Parallel lines and a transversal.
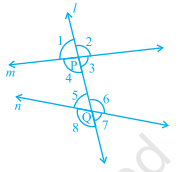
(a) Corresponding angles :
(i) ∠ 1 and ∠ 5 (ii) ∠ 2 and ∠ 6
(iii) ∠ 4 and ∠ 8 (iv) ∠ 3 and ∠ 7
(b) Alternate interior angles :
(i) ∠ 4 and ∠ 6 (ii) ∠ 3 and ∠ 5
(c) Alternate exterior angles:
(i) ∠ 1 and ∠ 7 (ii) ∠ 2 and ∠ 8
(d) Interior angles on the same side of the transversal:
(i) ∠ 4 and ∠ 5 (ii) ∠ 3 and ∠ 6.
- If a transversal intersects two parallel lines, then
(i) each pair of corresponding angles is equal,
(ii) each pair of alternate interior angles is equal,
(iii) each pair of interior angles on the same side of the transversal is supplementary.
- If a transversal intersects two lines such that, either
(i) any one pair of corresponding angles is equal, or
(ii) any one pair of alternate interior angles is equal, or
(iii) any one pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.
NCERT Class 9 Maths Chapter 6 Lines And Angles :
Class 9 Maths Exercise 6.2 (Page-80)
Q1. In Fig. 6.23, if AB \(\displaystyle \parallel \) CD, CD \(\displaystyle \parallel \) EF and y : z = 3 : 7, find x.
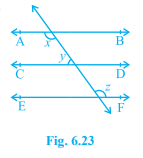
Solution :
According to the question,
Let the y = 3x
Let the z = 7x
Given = y = 3x
z = 7x
AB \(\displaystyle \parallel \) CD, CD \(\displaystyle \parallel \) EF
To prove = find x
Prove = z = x [ because, Vertically opposite angle ]
⇒ x = 7x
Now, x + y = 180\(\displaystyle ^{\circ }\) ( Alternate interior angle )
⇒ 7x + 3x = 180\(\displaystyle ^{\circ }\)
⇒ 10x = 180\(\displaystyle ^{\circ }\)
⇒ x = \(\displaystyle \frac{{{{{180}}^{\circ }}}}{{10}}\)
⇒ x = 18\(\displaystyle {^{\circ }}\)
So, 7x = 7 × 18\(\displaystyle {^{\circ }}\) = 126\(\displaystyle {^{\circ }}\)
⇒ x = z = 126\(\displaystyle {^{\circ }}\)
∴ Hence proved .
Q2. In fig. 6.24, if AB \(\displaystyle \parallel \) CD, EF \(\displaystyle \bot \) CD and \(\displaystyle \angle \)GED = 126\(\displaystyle ^{\circ }\), find \(\displaystyle \angle \)AGE, \(\displaystyle \angle \)GEF and \(\displaystyle \angle \)FGE.
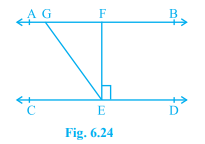
Solution :
According to the question,
Given = \(\displaystyle \angle \)GED = 126\(\displaystyle ^{\circ }\)
AB \(\displaystyle \parallel \) CD, EF \(\displaystyle \bot \) CD
To prove = \(\displaystyle \angle \)AGE, \(\displaystyle \angle \)GEF and \(\displaystyle \angle \)FGE
Prove = \(\displaystyle \angle GED\,=\,\angle AGE\)
⇒ \(\displaystyle \angle AGE\) = 126\(\displaystyle ^{\circ }\)
Now, \(\displaystyle \angle GEF\,+\,\angle FED\,=\,\angle GED\)
⇒ \(\displaystyle \angle GEF\) + 90\(\displaystyle ^{\circ }\) = 126\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEF\) = 126\(\displaystyle ^{\circ }\) - 90\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEF\) = 36\(\displaystyle ^{\circ }\)
So, CD is a line
⇒ \(\displaystyle \angle GEC\,=\,\angle FGE\) [ Alternate interior angle ]
⇒ \(\displaystyle \angle GEC\,+\,\angle GEF\,+\,\angle FED\) = 180\(\displaystyle ^{\circ }\) ( Straight line/Linear pair )
⇒ \(\displaystyle \angle GEC\,+\,\angle GEF\,+\,\angle FED\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEC\) + 36\(\displaystyle ^{\circ }\) + 90\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEC\) + 126\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEC\) = 180\(\displaystyle ^{\circ }\) - 126\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEC\) = 54\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle GEC\,=\,\angle FGE\) = 54\(\displaystyle ^{\circ }\)
∴ Hence proved .
Q3. In Fig. 6.25, if PQ \(\displaystyle \parallel \) ST, \(\displaystyle \angle PQR\,=\,{{110}^{\circ }}\) and \(\displaystyle \angle RST\,=\,{{130}^{\circ }}\) , find \(\displaystyle \angle QRS\).
[ Hint : Draw a line parallel to ST through point R.]
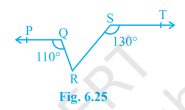
Solution :
According to the question,
Construct a line to XY parallel PQ
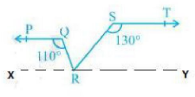
Given = \(\displaystyle \angle PQR\,=\,{{110}^{\circ }}\)
\(\displaystyle \angle RST\,=\,{{130}^{\circ }}\)
PQ \(\displaystyle \parallel \) ST
To prove = \(\displaystyle \angle QRS\)
Prove = \(\displaystyle \angle PQR\,+\,\angle QRX\,\) = 180\(\displaystyle ^{\circ }\) ( Linear pair )
⇒ 110\(\displaystyle ^{\circ }\) + \(\displaystyle \angle QRX\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle QRX\) = 180\(\displaystyle ^{\circ }\) - 110\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle QRX\) = 70\(\displaystyle ^{\circ }\)
So, \(\displaystyle \angle RST\,+\,\angle SRY\,\) = 180\(\displaystyle ^{\circ }\) ( Linear pair )
⇒ 130\(\displaystyle ^{\circ }\) + \(\displaystyle \angle SRY\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle SRY\) = 180\(\displaystyle ^{\circ }\) - 130\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle SRY\) = 50\(\displaystyle ^{\circ }\)
Now, the linear pair on the line XY
⇒ \(\displaystyle \angle QRX\,+\,\angle QRS\,+\,\angle SRY\,=\,{{180}^{\circ }}\) ( Linear pair )
⇒ 70\(\displaystyle ^{\circ }\) + \(\displaystyle \angle QRS\) + 50\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle QRS\) + 120\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle QRS\) = 180\(\displaystyle ^{\circ }\) - 120\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle QRS\) = 60\(\displaystyle ^{\circ }\)
∴ Hence proved .
Q4. In Fig. 6.32, if AB \(\displaystyle \parallel \) CD, \(\displaystyle \angle APQ\,=\,{{50}^{\circ }}\) and \(\displaystyle \angle PRD\,=\,{{127}^{\circ }}\) , find x and y.
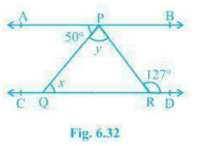
Solution :
According to the question,
Given = \(\displaystyle \angle APQ\,=\,{{50}^{\circ }}\)
\(\displaystyle \angle PRD\,=\,{{127}^{\circ }}\)
AB \(\displaystyle \parallel \) CD
To prove = find x and y
Prove = \(\displaystyle \angle PQR\,=\,\angle APQ\)
⇒ x = \(\displaystyle \angle APQ\)
⇒ x = 50\(\displaystyle ^{\circ }\) ( Alternate interior angle )
Now, \(\displaystyle \angle APR\,=\,\angle PRD\) ( Alternate interior angle )
⇒ \(\displaystyle \angle APQ\,=\,\angle QPR\) = 127\(\displaystyle ^{\circ }\) ( Alternate interior angle )
⇒ 50\(\displaystyle ^{\circ }\) + y = 127\(\displaystyle ^{\circ }\)
⇒ y = 127\(\displaystyle ^{\circ }\) - 50\(\displaystyle ^{\circ }\)
⇒ y = 77\(\displaystyle ^{\circ }\)
∴ Hence proved .
Q5. In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB \(\displaystyle \parallel \) CD.
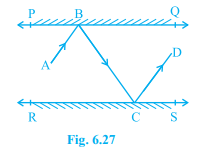
Solution :
According to the question,
Given = PQ and RS are two mirrors placed parallel to each other
An incident ray AB strikes the mirror PQ at B
the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD
To prove = AB \(\displaystyle \parallel \) CD
Prove = draw to line BE and CF, such that BE \(\displaystyle \bot \) PQ and CF \(\displaystyle \bot \) RS. 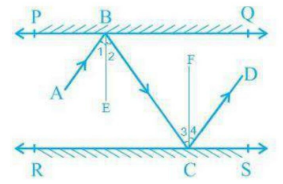
Since, PQ \(\displaystyle \parallel \) RS
BE \(\displaystyle \parallel \) CF
⇒ \(\displaystyle \angle 1\) = \(\displaystyle \angle 2\) [ Angle of incidence = Angle of reflection { By the law of reflection } ]
⇒ \(\displaystyle \angle 3\) = \(\displaystyle \angle 4\)
So, \(\displaystyle \angle 2\) = \(\displaystyle \angle 3\) ( Alternate interior angle )
Now, \(\displaystyle \angle 1\,+\,\angle 2\,=\,\angle 3\,+\,\angle 4\) ( Alternate interior angle )
Than, \(\displaystyle \angle ABC\,=\,\angle BCD\)
∴ AB \(\displaystyle \parallel \) CD, because ( Alternate interior angle are equal )
∴ Hence proved .