NCERT Solutions Class 9 Maths Chapter 6 Lines And Angles Exercise 6.1
Introduction:
In this exercise/article we will learn about Lines And Angles. Recall that a part (or portion) of a line with two end points is called a line-segment and a part of a line with one end point is called a ray. Note that the line segment AB is denoted by \(\displaystyle \overline{{AB}}\) , and its length is denoted by AB. The ray AB is denoted by \(\displaystyle \overrightarrow{{AB}}\) , and a line is denoted by \(\displaystyle \overleftrightarrow{{AB}}\).
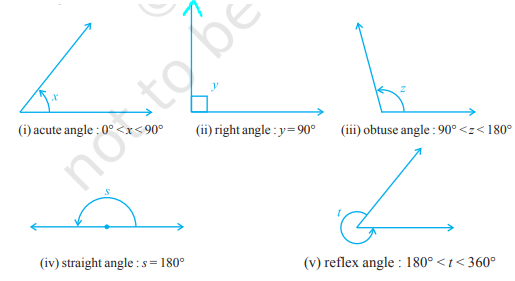
(i) An acute angle measures between 0\(\displaystyle ^{\circ }\) and 90\(\displaystyle ^{\circ }\)
(ii) A right angle is exactly equal to 90\(\displaystyle ^{\circ }\)
(iii) An angle greater than 90\(\displaystyle ^{\circ }\) but less than 180\(\displaystyle ^{\circ }\) is called an obtuse angle.
(iv) A striaght angle is equal to 180\(\displaystyle ^{\circ }\)
(v) An angle which is greater than 180\(\displaystyle ^{\circ }\) but less than 360\(\displaystyle ^{\circ }\) is called a reflex angle.
Further, two angles whose sum is 90\(\displaystyle ^{\circ }\) are called complementary angles, and two angles whose sum is 180\(\displaystyle ^{\circ }\) are called supplementary angles.
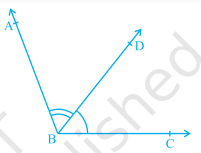
- Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms areon different sides of the common arm.
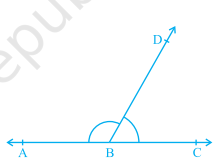
- If the non–common arms BA and BC in, form a line then it will look like. In this case, ∠ ABD and ∠ DBC are called linear pair of angles.
- You may also recall the vertically opposite angles formed when two lines, say AB and CD,
intersect each other, say at the point o.There are two pairs of vertically opposite angles.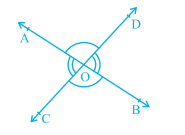
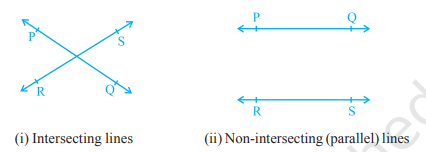
- Recall the notion of a line, that it extends indefinitely in both directions. Lines PQ and RS in (i) are intersecting lines and in (ii) are parallel lines. Note that the lengths of the common perpendiculars at different points on these parallel lines is the same. This equal length is called the distance between two parallel lines.
NCERT Class 9 Maths Chapter 6 Lines And Angles :
Class 9 Maths Exercise 6.1 (Page-76)
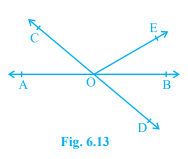
Q1. In fig. 6.13, lines AB and CD intersect at 0. If \(\displaystyle \angle AOC\) + \(\displaystyle \angle BOE\) = \(\displaystyle {{70}^{\circ }}\) and \(\displaystyle \angle BOD\) = \(\displaystyle {{40}^{\circ }}\) , find \(\displaystyle \angle BOE\) and reflex \(\displaystyle \angle COE\).
Solution :
According to the question,
Given = Lines AB and CD intersect at 0
\(\displaystyle \angle AOC\) + \(\displaystyle \angle BOE\) = \(\displaystyle {{70}^{\circ }}\)
\(\displaystyle \angle BOD\) = \(\displaystyle {{40}^{\circ }}\)
To prove = \(\displaystyle \angle BOE\) and reflex \(\displaystyle \angle COE\)
Prove = AB is a line
⇒ \(\displaystyle \angle AOC\) + \(\displaystyle \angle COE\) + \(\displaystyle \angle BOE\) = \(\displaystyle {{70}^{\circ }}\) = 180\(\displaystyle ^{\circ }\) ( Straight line/Linear pair )
⇒ \(\displaystyle \angle AOC\) + \(\displaystyle \angle BOE\) = \(\displaystyle {{70}^{\circ }}\) + \(\displaystyle \angle COE\) = 180\(\displaystyle ^{\circ }\)
⇒ 70\(\displaystyle ^{\circ }\) + \(\displaystyle \angle COE\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle COE\) = 180\(\displaystyle ^{\circ }\) - 70\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle COE\) = 110\(\displaystyle ^{\circ }\)
Than, CD is a line
⇒ \(\displaystyle \angle COE\) + \(\displaystyle \angle BOE\) + \(\displaystyle \angle BOD\) = 180\(\displaystyle ^{\circ }\) ( Straight line/Linear pair )
⇒ 110\(\displaystyle ^{\circ }\) + \(\displaystyle \angle BOE\) + 40\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle BOE\) + 110\(\displaystyle ^{\circ }\) + 40\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle BOE\) + 150\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle BOE\) = 180\(\displaystyle ^{\circ }\) - 150\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle BOE\) = 30\(\displaystyle ^{\circ }\)
Now, Reflex Angle = 360\(\displaystyle ^{\circ }\)
⇒ Reflex Angle - \(\displaystyle \angle COE\)
⇒ 360\(\displaystyle ^{\circ }\) - 110\(\displaystyle ^{\circ }\)
⇒ 250\(\displaystyle ^{\circ }\)
∴ Hence proved .
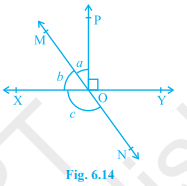
Q2. In Fig. 6.14, lines XY and MN intersect at 0. If \(\displaystyle \angle POY\) = 90\(\displaystyle ^{\circ }\) and a : b = 2 : 3. find c.
Solution :
According to the question,
Let the a = 2x
Let the b = 3x
Given = Lines XY and MN intersect at 0
\(\displaystyle \angle POY\) = 90\(\displaystyle ^{\circ }\)
To prove = c
Prove = XY is a line
⇒ \(\displaystyle \angle XOM\,+\,\angle MOP\,+\,\angle POY\) = 180\(\displaystyle ^{\circ }\) ( Straight line/Linear pair )
⇒ b + a + 90\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ 3x + 2x + 90\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ 3x + 2x = 180\(\displaystyle ^{\circ }\) - 90\(\displaystyle ^{\circ }\)
⇒ 5x = 90\(\displaystyle ^{\circ }\)
⇒ x = \(\displaystyle \frac{{{{{90}}^{\circ }}}}{5}\)
⇒ x = 18\(\displaystyle ^{\circ }\)
Hence, a = 2x = 2 × 18\(\displaystyle ^{\circ }\) = 36\(\displaystyle ^{\circ }\)
⇒ b = 3x = 3 × 18\(\displaystyle ^{\circ }\) = 54\(\displaystyle ^{\circ }\)
Now, MN is a line
⇒ \(\displaystyle \angle XOM\,+\,\angle XON\) = 180\(\displaystyle {^{\circ }}\) ( Linear pair )
⇒ b + c = 180\(\displaystyle {^{\circ }}\)
⇒ 54\(\displaystyle {^{\circ }}\) + c = 180\(\displaystyle {^{\circ }}\)
⇒ c = 180\(\displaystyle {^{\circ }}\) - 54\(\displaystyle {^{\circ }}\)
⇒ c = 126\(\displaystyle {^{\circ }}\)
∴ Hence proved .
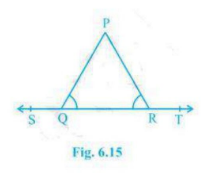
Q3. In Fig. 6.15, \(\displaystyle \angle PQR\,=\,\angle PRQ\), then prove that \(\displaystyle \angle PQS\,=\,\angle PRT\).
Solution :
According to the question,
Given = \(\displaystyle \angle PQR\,=\,\angle PRQ\)
To prove = \(\displaystyle \angle PQS\,=\,\angle PRT\)
Prove = ST is a line
⇒ \(\displaystyle \angle PQS\,+\,\angle PQR\) = 180\(\displaystyle ^{\circ }\) ( Linear line ) ...( 1 ) equation
⇒ \(\displaystyle \angle PRQ\,+\,\angle PRT\) = 180\(\displaystyle ^{\circ }\) ( Linear line ) ...( 2 ) equation
Now, From ( 1 ) equation and ( 2 ) equation
⇒ \(\displaystyle \angle PQS\,+\,\angle PQR\) = \(\displaystyle \angle PRQ\,+\,\angle PRT\)
⇒ \(\displaystyle \angle PQS\,+\,\angle PQR\) = \(\displaystyle \angle PQR\,+\,\angle PRT\) ( given )
⇒ \(\displaystyle \angle PQS\,+\,\angle PQR\) - \(\displaystyle \angle PQR\,=\,\angle PRT\)
⇒ \(\displaystyle \angle PQS\,=\,\angle PRT\)
∴ Hence proved .
Q4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
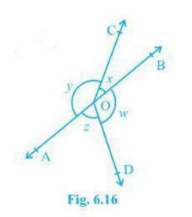
Solution :
According to the question,
Given = x + y = w + z
To prove = AOB is a line
Prove = The sum of all angles = 360\(\displaystyle ^{\circ }\)
⇒ x + y + w + z = 360\(\displaystyle ^{\circ }\)
⇒ ( x + y ) + ( w + z ) = 360\(\displaystyle ^{\circ }\)
⇒ ( x + y ) + ( x + y ) = 360\(\displaystyle ^{\circ }\) ( because, given x + y = w + z )
⇒ 2x + 2y = 360\(\displaystyle ^{\circ }\)
⇒ 2 ( x + y ) = 360\(\displaystyle ^{\circ }\)
⇒ x + y = \(\displaystyle \frac{{{{{360}}^{\circ }}}}{2}\)
⇒ x + y = 180\(\displaystyle ^{\circ }\)
∴ \(\displaystyle \angle AOC\,+\,\angle COB\) are forming linear pair. \(\displaystyle \angle AOB\) is a straight line.
Q5. In Fig. 6.17 , POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
\(\displaystyle \angle \)ROS = \(\displaystyle \frac{1}{2}\)( \(\displaystyle \angle \)QOS - \(\displaystyle \angle \)POS ).
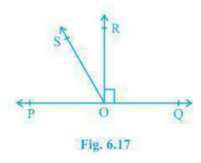
Solution :
According to the question,
Given = POQ is a line
Ray OR is perpendicular to line PQ
To prove = \(\displaystyle \angle \)ROS = \(\displaystyle \frac{1}{2}\)( \(\displaystyle \angle \)QOS - \(\displaystyle \angle \)POS )
Prove = Ray POQ is a straight line
but, OR \(\displaystyle \bot \) PQ
⇒ \(\displaystyle \angle \)POS + \(\displaystyle \angle \)ROS + \(\displaystyle \angle \)QOS = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle \)POS + \(\displaystyle \angle \)ROS + 90\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle \)POS + \(\displaystyle \angle \)ROS = 180\(\displaystyle ^{\circ }\) - 90\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle \)POS + \(\displaystyle \angle \)ROS = 90\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle \)ROS = 90\(\displaystyle ^{\circ }\) - \(\displaystyle \angle \)POS ...(1) equation
Now, \(\displaystyle \angle \)ROS + \(\displaystyle \angle \)ROQ = \(\displaystyle \angle \)QOS
⇒ \(\displaystyle \angle \)ROS + 90\(\displaystyle ^{\circ }\) = \(\displaystyle \angle \)QOS
⇒ \(\displaystyle \angle \)ROS = \(\displaystyle \angle \)QOS - 90\(\displaystyle ^{\circ }\) ...(2) equation
Than, Adding equation 1 and 2 ,
⇒ \(\displaystyle \angle \)ROS + \(\displaystyle \angle \)ROS = 90\(\displaystyle ^{\circ }\) - \(\displaystyle \angle \)POS + \(\displaystyle \angle \)QOS - 90\(\displaystyle ^{\circ }\)
⇒ 2\(\displaystyle \angle \)ROS = \(\displaystyle \angle \)QOS - \(\displaystyle \angle \)POS
⇒ \(\displaystyle \angle \)ROS = \(\displaystyle \frac{1}{2}\)( \(\displaystyle \angle \)QOS - \(\displaystyle \angle \)POS )
∴ Hence proved .
Q6. It is given that \(\displaystyle \angle XYZ\) = 64\(\displaystyle ^{\circ }\) and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects \(\displaystyle \angle ZYP\) , find \(\displaystyle \angle XYQ\) and reflex \(\displaystyle \angle QYP\).
Solution :
Draw the figure according to the question,
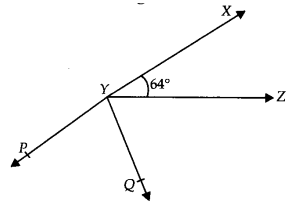
Given = \(\displaystyle \angle XYZ\) = 64\(\displaystyle ^{\circ }\)
To prove = Ray YQ bisects \(\displaystyle \angle ZYP\) , find \(\displaystyle \angle XYQ\) and reflex \(\displaystyle \angle QYP\)
Prove = \(\displaystyle \angle \)XYP is a line
⇒ \(\displaystyle \angle PYZ\,+\,\angle XYZ\) = 180\(\displaystyle ^{\circ }\) ( Linear pair )
⇒ \(\displaystyle \angle PYZ\) + 64\(\displaystyle ^{\circ }\) = 180\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle PYZ\) = 180\(\displaystyle ^{\circ }\) - 64\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle PYZ\) = 116\(\displaystyle ^{\circ }\)
Since, \(\displaystyle \angle ZYP\) is bisect by ray YQ
Let the \(\displaystyle \angle PYQ\,=\,\angle ZYQ\)
⇒ \(\displaystyle \angle PYQ\,=\,\angle ZYQ\,=\,\frac{1}{2}\angle PYZ\)
⇒ \(\displaystyle \angle PYQ\,=\,\angle ZYQ\,=\,\frac{1}{2}\times \,{{116}^{\circ }}\)
⇒ \(\displaystyle \angle ZYQ\,=\,{{58}^{\circ }}\)
⇒ \(\displaystyle \angle XYQ\,=\,\angle XYZ\,+\,\angle ZYQ\)
⇒ \(\displaystyle \angle XYQ\,= 64\)latex \displaystyle ^{\circ }$ + 58\(\displaystyle ^{\circ }\)
⇒ \(\displaystyle \angle XYQ\) = 122\(\displaystyle ^{\circ }\)
So, Reflex angle = 360\(\displaystyle ^{\circ }\)
⇒ Reflex angle - \(\displaystyle \angle QYP\)
⇒ 360\(\displaystyle ^{\circ }\) - 58\(\displaystyle ^{\circ }\)
⇒ 302\(\displaystyle ^{\circ }\)
∴ Hence proved.