NCERT Solutions Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1
Introduction:
In this exercise/article we will learn about Coordinate Geometry. You observed that the axes ( plural of the word axis' ) divide the plane into four part are called the quadrants ( one fourth part ), numbered I, II ,III and IV anticlockwise from OX. So, the plane consists of the axes and these quadrants. We call the plane, the Cartesian plane, or the coordinate plane, or the xy-plane. The axes are called the coordinate axes.
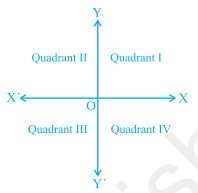
NCERT Class 9 Maths Chapter 3 Coordinate Geometry :
- NCERT Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1
- NCERT Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2
Class 9 Maths Exercise 3.1 (Page-45)
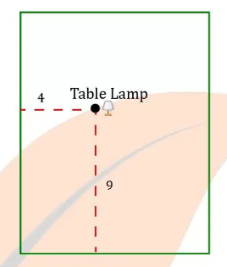
Q1. How will you describe the position of a table lamp on your study table to another person ?
Solution :
The position of a table lamp on my study table is 9 unit far the wall and 4 unit far of the sitting place .
Q2. (Street plan): A city has two main roads which cross which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are about 5 street in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North-South direction and 5th
in the East-West direction meet at some crossing, then will call this cross-street (2,5). Using this convention, find :
(i) how many cross-streets can be referred to as (4,3).
(ii) how many cross-streets can be referred to as (3,4).
Solution :
(i) One cross-streets can be referred by the point A (4,3).
(ii) One cross-streets can be referred by the point B (3,4).

