NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume

Introduction :

In this chapter we will learn about Surface Area And Volume. It would be interesting to see what happens if we cut out many of these plane figures of the same shape and size from cardboard sheet and stack them up in a vertical pile. By this process, we shall obtain some solid figures (briefly called solids) such as a cuboid, a cylinder, etc. In the earlier classes, you have also learnt to find the surface areas and volumes of cuboids, cubes and cylinders. We shall now learn to find the surface areas and volumes of cuboids and cylinders in details and extend this study to some other solids such as cones and spheres.

Class 9 Maths Chapter 13 Surface Area And Volume :

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.1

In this exercise-13.1 we will learn about Surface Area And Volume. Surface Area of a cuboid and cube, Surface area of a cube . Lateral surface area and total surface area of the cuboid . this exercise based only on cube and cuboid formula . you know that cube and cuboid shows 3D picture of square and rectangle. In such a case , the area of these four faces is called the lateral surface area.

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.2

In this exercise-13.2 we will learn about Surface Area And Volume. Surface area of a Right Circular Cylinder. Curved surface area and Total surface area of a cylinder. this exercise based only on cylinder of formula. You know π = 227. Here, we will be dealing with only right circular cylinders. So, unless started otherwise, the word cylinder would means a right circular cylinder. In the case of a cylinder, unless started otherwise, 'Radius of a cylinder' will mean 'base radius of the cylinder '.

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.3

In this exercise-13.3 we will learn about Surface Area And Volume. Surface area of a Right Circular Cone, Curved surface area of a cone and total surface area of cone. So far, we have been generating solids by stacking up congruent figures. Incidentally, such figures are called Prisms. Now let us look at another kind of solids which is not a prism. (These kinds of solids are called Pyramids).

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.4

In this exercise-13.4 we will learn about Surface Area And Volume. Surface area of a sphere. You can say ,because a circle is a plan closed figure whose every point lies at a constant distance (called radius) from a fixed point, which is called the centre of the circle. So, it is called a sphere. Curved surface of a hemisphere and total surface area of hemisphere. It gets divided into two equal part, What will each half be called? it is called a hemisphere. ( because 'hemi' also means 'half' ).

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.5

In this exercise-13.5 we will learn about Surface Area And Volume. Volume of cuboid and cube .If an object is solid, then the space occupied by such an object is measured, and it termed the Volume of the object. On the other hand, if the object is hollow, then interior is empty, and can be filled with air, or some liquid that will take the shape of its container. In this case, the volume of the substance that can fill the interior is called the capacity of the container. In short, the volume of an object is the measure of the space it occupies, and the capacity of an object is the volume of substance its interior can accommodate.

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.6

In this exercise-13.6 we will learn about Surface Area And Volume. Volume of a cylinder . Just as a cuboid is built up with rectangles of the same size, we have seen that a right circular cylinder can be built up using circles of the same size. So, using the same aargument as for a cuboid, we can see that the volume of a cylinder can be obtained as : base area × height, where r is the base radius and h is the height of the cylinder.

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.7

In this exercise-13.7 we will learn about Surface Area And Volume. Volume of a right circular cone. Try to make a hollow cylinder and a hollow cone like this with the same base radius and the same height. Then, we can try out an experiment that will help us, to see practically what the volume of a right circular cone would be!

So, let us start like this.
Fill the cone up to the brim with sand once, and empty it into the cylinder. We find that it fills up only a part of the cylinder. When we fill up the cone again to the brim, and empty it into the cylinder, we see that the cylinder is still not full. When the cone is filled up for the third time, and emptied into the cylinder, it can be seen that the cylinder is also full to the brim. With this, we can safely come to the conclusion that three times the volume of a cone, makes up the volume of a cylinder, which has the same base radius and the same height as the cone, which means that the volume of the cone is one-third the volume of the cylinder.

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.8

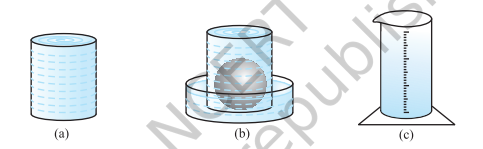
In this exercise-13.8 we will learn about Surface Area And Volume. Volume of sphere and hemisphere . Since a hemisphere is half of a sphere. Let us see how to go about measuring the volume of a sphere. First, take two or three spheres of different radii, and a container big enough to be able to put each of the spheres into it, one at a time. Also, take a large trough in which you can place the container. The, fill the container up to the brim with water. Now, carefully place one of the spheres in the container. Some of the water from the container will over flow into the trough in which it is kept. Carefully pour out the water from the trough into a measuring cylinder (i.e., a graduated cylindrical jar) and measure the water over flowed. Suppose the radius of the immersed sphere is r (you can find the radius by measuring the diameter of the sphere). Then evaluate \(\displaystyle \frac{4}{3}\pi {{r}^{3}}\). Do you find this value almost equal to the measure of the volume over flowed ?