NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.8

Introduction:

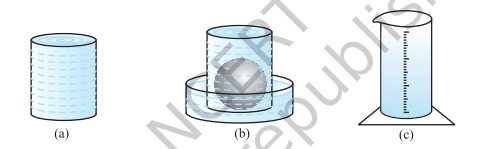
In this exercise/article we will learn about Surface Area And Volume. Volume of sphere and hemisphere . Since a hemisphere is half of a sphere. Let us see how to go about measuring the volume of a sphere. First, take two or three spheres of different radii, and a container big enough to be able to put each of the spheres into it, one at a time. Also, take a large trough in which you can place the container. The, fill the container up to the brim with water. Now, carefully place one of the spheres in the container. Some of the water from the container will over flow into the trough in which it is kept. Carefully pour out the water from the trough into a measuring cylinder (i.e., a graduated cylindrical jar) and measure the water over flowed. Suppose the radius of the immersed sphere is r (you can find the radius by measuring the diameter of the sphere). Then evaluate \(\displaystyle \frac{4}{3}\pi {{r}^{3}}\). Do you find this value almost equal to the measure of the volume over flowed ?

Class 9 Maths Chapter 13 Surface Area And Volume :

Class 9 Maths Exercise 13.8 (Page-236)

Q1. Find the volume of a sphere whose radius is

(i) 7 cm (ii) 0.63 m

Solution :

According to the question,

(i) Given, Radius = 7 cm

So, volume of a sphere = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 7 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 343

= \(\displaystyle \frac{{30184}}{{21}}\)

= 1437\(\displaystyle \frac{1}{3}\) cm3

∴ volume of sphere = 1437\(\displaystyle \frac{1}{3}\) cm3 .

(ii) Given, Radius = 0.63 m

So, volume of a sphere = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 0.63 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 0.25

= \(\displaystyle \frac{{22}}{{21}}\)

= 1.05 cm3 ( approx )

∴ volume of sphere = 1.05 m3 .

Q2. Find the amount of water displaced by a solid spherical ball of diameter

(i) 28 cm (ii) 0.21 m

Solution :

According to the question,

(i) Given, Diameter = 28 cm

R = \(\displaystyle \frac{d}{2}\)

R = \(\displaystyle \frac{{28}}{2}\)

R = 14 cm

So, volume of a sphere = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 14 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 2744

= \(\displaystyle \frac{{241472}}{{21}}\)

= 11498\(\displaystyle \frac{2}{3}\) cm3

∴ The amount of water displaced by a solid spherical ball = 11498\(\displaystyle \frac{2}{3}\) cm3 .

(ii) Given, Diameter = 0.12 m

R = \(\displaystyle \frac{d}{2}\)

R = \(\displaystyle \frac{{0.21}}{2}\)

R = 0.105 m

So, volume of a sphere = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 0.105 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 0.001157625

= \(\displaystyle \frac{{0.101871}}{{21}}\)

= 0.004851 m3

∴ The amount of water displaced by a solid spherical ball = 0.004851 m3 .

Q3. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3 ?

Solution :

According to the question,

Given, Diameter = 4.2

R = \(\displaystyle \frac{d}{2}\)

R = \(\displaystyle \frac{{4.2}}{2}\)

R = 2.1 cm

So, volume of a metallic ball = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 2.1 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 9.26

= \(\displaystyle \frac{{814.88}}{{21}}\)

= 38.808 cm3

Here, the density of the metal 1 cm3 = 8.9 g

Now, the density of the metal 38.808 cm3 = 38.808 × 8.9

= 345.39 g

∴ 345.39 g is the mass of the ball .

Q4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon ?

Solution :

According to the question,

Given, \(\displaystyle {{d}_{m}}\) = \(\displaystyle \frac{1}{4}{{d}_{e}}\)

\(\displaystyle {{r}_{m}}\) = \(\displaystyle \frac{1}{4}{{r}_{e}}\)

So, \(\displaystyle {{r}_{m}}\) = \(\displaystyle \frac{1}{4}{{r}_{e}}\)

⇒ 4\(\displaystyle {{r}_{m}}\) = \(\displaystyle {{r}_{e}}\)

Now, \(\displaystyle \frac{{volume\,of\,sphere\,moon}}{{volume\,of\,sphere\,earth}}\,=\,\frac{{\frac{4}{3}\pi {{r}_{m}}^{3}}}{{\frac{4}{3}\pi {{r}_{e}}^{3}}}\)

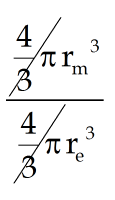
= \(\displaystyle \frac{{{{r}_{m}}^{3}}}{{{{r}_{e}}^{3}}}\)

= \(\displaystyle \frac{{{{r}_{m}}^{3}}}{{{{{(4{{r}_{m}})}}^{3}}}}\)

= \(\displaystyle \frac{{{{r}_{m}}^{3}}}{{64{{r}_{m}}^{3}}}\)

= \(\displaystyle \frac{1}{{64}}\)

∴ the volume of the moon is \(\displaystyle \frac{1}{{64}}\) the volume of earth .

Q5. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold ?

Solution :

According to the question,

Given, diameter = 10.5 cm

R = \(\displaystyle \frac{d}{2}\)

R = \(\displaystyle \frac{{10.5}}{2}\)

R = 5.25 cm

So, volume of a hemispherical bowl = \(\displaystyle \frac{2}{3}\)πr3

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 5.25 )3

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 144.70

= \(\displaystyle \frac{{6366.8}}{{21}}\)

= 303.18 cm3

⇒ Convert into cm3 to litre

= \(\displaystyle \frac{{303.18}}{{1000}}\)

= 0.303 litres ( approx )

∴ 0.303 litres of milk can hold of hemispherical bowl .

Q6. A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m. then find the volume of the iron used to make the tank .

Solution :

According to the question,

Given, Inner Radius = 1 m

thickness = 1 cm

thickness = 0.01 m [ converted cm to m ]

Outer radius = 1 + 0.01 = 1.01 m

So, volume of a hemispherical tank = \(\displaystyle \frac{2}{3}\)π ( R3 - r3 )

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 13 - 1.013 )

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 1 - 1.03 )

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 0.03

= \(\displaystyle \frac{{1.32}}{{21}}\)

= 0.0628 m3

∴ The volume of the iron used to make the tank = 0.0628 m3 .

Q7. Find the volume of a sphere whose surface area is 154 cm2 .

Solution :

According to the question,

Given, Surface area of sphere = 154 cm2

So, surface area of sphere = 4πr2

⇒ 154 = 4 × \(\displaystyle \frac{{22}}{7}\) × r2

⇒ 154 × 7 = 88r2

⇒ 1078 = 88r2

⇒ \(\displaystyle \frac{{1078}}{{88}}\) = r2

⇒ 12.25 = r2

⇒ 3.5 cm

Now, volume of a sphere = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 3.5 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 42.875

= \(\displaystyle \frac{{3773}}{{21}}\)

= 179\(\displaystyle \frac{2}{3}\) cm3

∴ The volume of a sphere = 179\(\displaystyle \frac{2}{3}\) cm3 .

Q8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs 4989.60 . If the cost of white-washing is Rs 20.00 per square meter, find the

(i) inside surface area of the dome, (ii) volume of the air inside the dome .

Solution :

According to the question,

(i) Given, The rate of white-washing is Rs 20.00 per square meter

From inside, it was white-washed at the cost of Rs 4989.60

So, Cost = Rate × Area

⇒ 4989.60 = 20 × Area

⇒ \(\displaystyle \frac{{4989.60}}{{20}}\) = Area

⇒ 249.48 m2 = Area

∴ Inside surface area of the dome = 249.48 m2

Now, Curved surface area of hemisphere = 2πr2

⇒ 2πr2 = 249.48

⇒ 2 × \(\displaystyle \frac{{22}}{7}\) × r2\ = 249.48

⇒ 2 × 22 × r2\ = 249.48 × 7

⇒ 44r2 = 1746.36

⇒ r2 = \(\displaystyle \frac{{1746.36}}{{44}}\)

⇒ r2 = 39.69

⇒ r = \(\displaystyle \sqrt{{39.69}}\)

⇒ r = 6.3 m

(ii) Volume of the air inside the dome = \(\displaystyle \frac{2}{3}\pi {{r}^{3}}\)

= \(\displaystyle \frac{2}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 6.3 × 6.3 × 6.3

= \(\displaystyle \frac{{11002.068}}{{21}}\)

= 523.908 m3

∴ Volume of the air inside the dome = 523.908 m3 .

Q9. Twenty seven soild iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S' . Find the

(i) radius r' of the new sphere , (ii) ratio of S and S' .

Solution :

According to the question,

(i) Given, Radius of soild iron spheres = r

Radius of soild iron new spheres = r'

So, volume of solid sphere = \(\displaystyle \frac{4}{3}\)πr3

The volume of 27 solid sphere = 27 × \(\displaystyle \frac{4}{3}\)πr3

Now, volume of new sphere = volume of 27 solid sphere

⇒ \(\displaystyle \frac{4}{3}\)π(r')3 = 27 × \(\displaystyle \frac{4}{3}\)πr3

⇒ (r')3 = 27 × \(\displaystyle \frac{4}{3}\)πr3 × \(\displaystyle \frac{4}{3}\pi \)

⇒ (r')3 = 27 × r3

⇒ (r')3 = 27r3

⇒ r' = 3r

∴ The radius r' of the new sphere = 3r

(ii) Given, Radius = 3r

So, surface area of solid sphere S = 4πr2

surface area of new sphere S' = 4π( r'2 )

= 4π( 3r )2

= 4π × 9r2

= 36πr2

∴ The ratio of S and S' = \(\displaystyle \frac{{4\pi {{r}^{2}}}}{{36\pi {{r}^{2}}}}\)

= \(\displaystyle \frac{1}{9}\)

∴ The ratio of S and S' = 1 : 9 .

Q10. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine ( in mm3 ) is needed to fill this capsule ?

Solution :

According to the question,

Given, Diameter = 3.5 mm

R = \(\displaystyle \frac{d}{2}\)

R = \(\displaystyle \frac{{3.5}}{2}\)

R = 1.75 mm

So, volume of capsule = \(\displaystyle \frac{4}{3}\)πr3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 1.75 )3

= \(\displaystyle \frac{4}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 5.35

= \(\displaystyle \frac{{470.8}}{{21}}\)

= 22.42 mm3 ( approx )

∴ Capsule medicine will need to fill this capsule = 22.42 mm3 .

Class 9 Maths Chapter 13 Surface Area And Volume :

NCERT Solutions Class 9 Maths Chapter 13 Surface Area And Volume Exercise 13.8

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.8

Introduction:

Class 9 Maths Exercise 13.8 (Page-236)

Leave a Comment Cancel Reply