NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.7

Introduction:

In this exercise/article we will learn about Surface Area And Volume. Volume of a right circular cone. Try to make a hollow cylinder and a hollow cone like this with the same base radius and the same height. Then, we can try out an experiment that will help us, to see practically what the volume of a right circular cone would be!

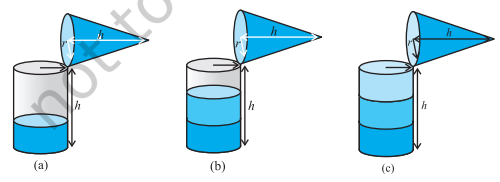
So, let us start like this.
Fill the cone up to the brim with sand once, and empty it into the cylinder. We find that it fills up only a part of the cylinder. When we fill up the cone again to the brim, and empty it into the cylinder, we see that the cylinder is still not full. When the cone is filled up for the third time, and emptied into the cylinder, it can be seen that the cylinder is also full to the brim. With this, we can safely come to the conclusion that three times the volume of a cone, makes up the volume of a cylinder, which has the same base radius and the same height as the cone, which means that the volume of the cone is one-third the volume of the cylinder.

Class 9 Maths Chapter 13 Surface Area And Volume :

Class 9 Maths Exercise 13.7 (Page-233)

Q1. Find the volume of the right circular cone with

(i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm

Solution :

According to the question,

(i) Given, Radius = 6 cm

Height = 7 cm

So, volume of right circular cone = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 6 )2 × 7

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 36 × 7

= \(\displaystyle \frac{{5544}}{{21}}\)

= 264 cm2

∴ The volume of the right circular cone = 264 cm2

(ii) Given, Radius = 3.5 cm

Height = 12 cm

So, volume of right circular cone = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 3.5 )2 × 12

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 12.25 × 12

= \(\displaystyle \frac{{3234}}{{21}}\)

= 154 cm2

∴ The volume of the right circular cone = 154 cm2 .

Q2. Find the capacity in litres of a conical vessel with

(i) radius 7 cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm

Solution :

According to the question,

(i) Given, Radius = 7 cm

Slant height = 25 cm

Slant height = h = \(\displaystyle \sqrt{{{{r}^{2}}\,-\,{{l}^{2}}}}\)

⇒ h = \(\displaystyle \sqrt{{{{7}^{2}}\,-\,{{{25}}^{2}}}}\)

⇒ h = \(\displaystyle \sqrt{{49\,-\,625}}\)

⇒ h = \(\displaystyle \sqrt{{576}}\) [ using long division method ]

⇒ h = 24

So, volume of conical vessel = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 7 )2 × 24

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 49 × 24

= \(\displaystyle \frac{{25872}}{{21}}\)

= 1232 cm2

= 1.232 litres [ converted cm to litre ]

∴ The capacity in litres of a conical vessel = 1.232 litres

(ii) Given, Height = 12 cm

Slant height = 13 cm

Slant height = r = \(\displaystyle \sqrt{{{{h}^{2}}\,-\,{{l}^{2}}}}\)

⇒ r = \(\displaystyle \sqrt{{{{{12}}^{2}}\,-\,{{{13}}^{2}}}}\)

⇒ r = \(\displaystyle \sqrt{{144\,-\,169}}\)

⇒ r = \(\displaystyle \sqrt{{25}}\) [ using long division method ]

⇒ r = 5

So, volume of conical vessel = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 5 )2 × 12

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 25 × 12

= \(\displaystyle \frac{{6600}}{{21}}\)

= \(\displaystyle \frac{{6600}}{{21\,\times \,1000}}\) [ convert cm to litre ]

= \(\displaystyle \frac{{11}}{{35}}\)

∴ The capacity in litres of a conical vessel = \(\displaystyle \frac{{11}}{{35}}\) litres .

Q3. The height of a cone is 15 cm. If its volume is 1570 cm3, Find the radius of the base. ( Use π = 3.14 )

Solution :

According to the question,

Given, Height = 15 cm

Volume of cone = 1570 cm3

So, volume of a cone = \(\displaystyle \frac{1}{3}\)πr2h

⇒ 1570 = \(\displaystyle \frac{1}{3}\) × 3.14 × r2 × 15

⇒ 1570 × 3 = 3.14 × r2 × 15

⇒ 4710 = 47.1r2

⇒ \(\displaystyle \frac{{4710}}{{47.1}}\) = r2

⇒ 100 = r2

⇒ \(\displaystyle \sqrt{{100}}\) = r [ using long division method ]

⇒ 10 cm = r

∴ The radius of the base of cone = 10 cm .

Q4. If the volume of a right circular cone of height 9 cm is 48 π cm3, find the diameter of its base.

Solution :

According to the question,

Given, Height = 9 cm

Volume of a right circular cone = 48 π cm3

So, volume of a right circular cone = \(\displaystyle \frac{1}{3}\)πr2h

⇒ 48 π = \(\displaystyle \frac{1}{3}\) × π × r2 × 9

⇒ 48 π × 3 = π × r2 × 9

⇒ 144 π = 9πr2

⇒ \(\displaystyle \frac{{144\pi }}{{9\pi }}\) = r2

⇒ 16 = r2

⇒ \(\displaystyle \sqrt{{16}}\) = r

⇒ 4 = r

Now, the diameter of base = 2 × 4

= 8 cm

∴ The diameter of the right circular cone = 8 cm .

Q5. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres ?

Solution :

According to the question,

Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{3.5}}{2}\)

Radius = 1.75 m

Given, Radius = 1.75 m

Height/deep = 12 m

So, volume of conical pit = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 1.75 )2 × 12

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 3.0625 × 12

= \(\displaystyle \frac{{808.5}}{{21}}\)

= 38.5 m3

Now, 38.5 × 1 = 38.5 [ converted m3 to kl ]

∴ 38.5 kl is its capacity .

Q6. The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find

(i) height of the cone (ii) slant height of the cone

(iii) curved surface area of the cone

Solution :

According to the question,

Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{28}}{2}\)

Radius = 14 cm

(i) Given, Radius = 14 cm

volume of a right circular cone is 9856 cm3

So, volume of a cone = \(\displaystyle \frac{1}{3}\)πr2h

⇒ 9856 = \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 14 )2 × h

⇒ 9856 × 3 × 7 = 22 × 196 × h

⇒ 206976 = 4312h

⇒ \(\displaystyle \frac{{206976}}{{4312}}\) = h

⇒ 48 = h

∴ Height of the cone = 48 cm

(ii) Given, Radius = 14 cm

Height = 48 cm

So, slant height of the cone = l = \(\displaystyle \sqrt{{{{r}^{2}}\,+\,{{h}^{2}}}}\)

⇒ l = \(\displaystyle \sqrt{{{{{14}}^{2}}\,+\,{{{48}}^{2}}}}\)

⇒ l = \(\displaystyle \sqrt{{196\,+\,2304}}\)

⇒ l = \(\displaystyle \sqrt{{2500}}\) [ using long division method ]

⇒ l = 50

∴ Slant height of the cone = 50 cm

(iii) Given, Radius = 14 cm

slant height = 50 cm

So, curved surface area of the cone = πrl

= \(\displaystyle \frac{{22}}{7}\) × 14 × 50

= \(\displaystyle \frac{{15400}}{7}\)

= 2200 cm2

∴ Curved surface area of cone = 2200 cm2 .

Q7. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained .

Solution :

According to the figure,

Given, If the triangle is revolved about the side 12 cm

Radius = 5 cm

Height = 12 cm

slant height = 13 cm

So, volume of a cone = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × π × ( 5 )2 × 12

= \(\displaystyle \frac{1}{3}\) × π × 25 × 12

= \(\displaystyle \frac{{300}}{3}\)π

= 100π

∴ The volume of the solid cube is 100π .

Q8. If the triangle ABC in the question 7 above is revolved about the side 5 cm, find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in questions 7 and 8 .

Solution :

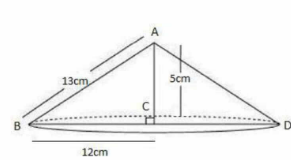
According to the figure,

Given, If the triangle is revolved about the side 5 cm

Radius = 12 cm

Height = 5 cm

slant height = 13 cm

So, volume of cone = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × π × ( 12 )2 × 5

= \(\displaystyle \frac{1}{3}\) × π × 144 × 5

= \(\displaystyle \frac{{720}}{3}\)π

= 240π

∴ The volume of the solid cube is 240π

Now, the ratio of the volumes of the two solids obtained in questions 7 and 8 = \(\displaystyle \frac{{100\pi }}{{240\pi }}\)

= \(\displaystyle \frac{5}{{12}}\)

= 5 : 12

∴ The ratio of the volumes of the two solids cubes = 5 : 12 .

Q9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.

Solution :

According to the question,

Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{10.5}}{2}\)

Radius = 5.25 m

Given, Radius = 5.25 m

Height = 3 m

So, volume of cone = \(\displaystyle \frac{1}{3}\)πr2h

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × ( 5.25 )2 × 3

= \(\displaystyle \frac{1}{3}\) × \(\displaystyle \frac{{22}}{7}\) × 27.5625 × 3

= \(\displaystyle \frac{{1819.125}}{{21}}\)

= 86.625 m3

Now, slant height = \(\displaystyle \sqrt{{{{r}^{2}}\,+\,{{h}^{2}}}}\)

= l = \(\displaystyle \sqrt{{{{{5.25}}^{2}}\,+\,{{3}^{2}}}}\)

= l = \(\displaystyle \sqrt{{27.5625\,+\,9}}\)

= l = \(\displaystyle \sqrt{{36.5625\,}}\)

= l = 6.05 m ( approx )

As, area of the canvas required = πrl

= \(\displaystyle \frac{{22}}{7}\) × 5.25 × 6.05

= \(\displaystyle \frac{{698.775}}{7}\)

= 99.825 m2

∴ The required area of canvas to protect wheat = 99.825 m2 .

Class 9 Maths Chapter 13 Surface Area And Volume :

NCERT Solutions Class 9 Maths Chapter 13 Surface Area And Volume Exercise 13.7

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.7

Introduction:

Class 9 Maths Exercise 13.7 (Page-233)

Leave a Comment Cancel Reply