NCERT Solutions Class 9 Maths Chapter 13 Surface Area And Volume Exercise 13.4

Leave a Comment / Class 9 Maths / By
Spread the love

NCERT Solutions Class 9 Maths Chapter 13 Surface area and Volume Exercise 13.4

 

Introduction:

In this exercise/article we will learn about Surface Area And Volume. Surface area of a sphere. You can say ,because a circle is a plan closed figure whose every point lies at a constant distance (called radius) from a fixed point, which is called the center of the circle. So, it is called a sphere. Curved surface of a hemisphere and total surface area of hemisphere. It gets divided into two equal part, What will each half be called? it is called a hemisphere. ( because 'hemi' also means 'half' ).

 

Class 9 Maths Chapter 13 Surface Area And Volume :

Class 9 Maths Exercise 13.4 (Page-225)

Q1. Find the surface area of a sphere of radius :

(i) 10.5 cm                      (ii) 5.6 cm                                (iii) 14 cm

Solution : 

According to the question,

(i) Given, Radius = 10.5 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 10.5 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 110.25

= \(\displaystyle \frac{{88}}{7}\) × 110.25

= \(\displaystyle \frac{{9702}}{7}\)

= 1386 cm2

∴ The surface area of a sphere = 1386 cm2

(ii) Given, Radius = 5.6 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 5.6 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 31.36

= \(\displaystyle \frac{{88}}{7}\) × 31.36

= \(\displaystyle \frac{{2759.68}}{7}\) 

= 394.24 cm2

∴ The surface area of a sphere = 394.24 cm2

(iii) Given, Radius = 14 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 14 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 196

= \(\displaystyle \frac{{88}}{7}\) × 196

= \(\displaystyle \frac{{17248}}{7}\) 

= 2464 cm2

∴ The surface area of a sphere = 2464 cm2 .

Q2. Find the total surface area of a sphere of diameter :

(i) 14 cm                   (ii) 21 cm                   (iii) 3.5 cm

Solution : 

According to the question,

(i) Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{14}}{2}\)

Radius = 7 cm

Given, Radius = 7 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 7 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 49

= \(\displaystyle \frac{{88}}{7}\) × 49

= \(\displaystyle \frac{{4312}}{7}\) 

= 616 cm2

∴ Total surface area of a sphere = 616 cm2

(ii) Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{21}}{2}\)

Radius = 10.5 cm

Given, Radius = 10.5 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 10.5 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 110.25

= \(\displaystyle \frac{{88}}{7}\) × 110.25

= \(\displaystyle \frac{{9702}}{7}\)

= 1386 cm2

∴ Total surface area of a sphere = 1386 cm2

(iii) Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{3.5}}{2}\)

Radius = 1.75 cm

Given, Radius = 1.75 cm

So, Surface area of a sphere = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 1.75 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 3.0625

= \(\displaystyle \frac{{88}}{7}\) × 3.0625

= \(\displaystyle \frac{{269.5}}{7}\)

= 38.5 cm2

∴ Total surface area of a sphere = 38.5 cm2 .

Q3. Find the total surface area of a hemisphere of radius 10 cm. ( Use π = 3.14 )

Solution :

According to the question,

Given, Radius = 10 cm

So, Surface area of a hemisphere = 3πr2

= 3 × 3.14 × ( 10 )2

= 3 × 3.14 × 100

= 9.42 × 100

= 942 cm2

∴ Total surface area of a hemisphere = 942 cm2 .

Q4. The radius of a spherical balloon increase from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface area of the balloon in the two cases.

Solution :

According to the question,

Case (i) 

Given, Radius = 7 cm

So, Surface area of the balloon = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 7 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 49

= \(\displaystyle \frac{{88}}{7}\) × 49

= \(\displaystyle \frac{{4312}}{7}\) 

= 616 cm2

∴ Surface area of the balloon = 616 cm2

Case (ii)

Given, Radius = 14 cm

So, Surface area of the balloon = 4πr2

= 4 × \(\displaystyle \frac{{22}}{7}\) × ( 14 )2

= 4 × \(\displaystyle \frac{{22}}{7}\) × 196

= \(\displaystyle \frac{{88}}{7}\) × 196

= \(\displaystyle \frac{{17248}}{7}\)

= 2464 cm2

∴ Surface area of the balloon = 2464 cm2

Now, Ratio of surface area of the balloon = \(\displaystyle \frac{{Case\,i}}{{Case\,ii}}\)

= \(\displaystyle \frac{{616}}{{2464}}\)

=

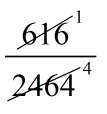
= \(\displaystyle \frac{1}{4}\)

∴ Ratio of surface area of the balloon = 1:4

Q5. A hemisphere bowl made of brass has inner daimeter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm2.

Solution : 

According to the question,

Radius = \(\displaystyle \frac{d}{2}\)

Radius = \(\displaystyle \frac{{10.5}}{2}\)

Radius = 5.25 cm

Given, Radius = 5.25 cm

So, Inner surface area of a sphere = 2πr2

= 2 × \(\displaystyle \frac{{22}}{7}\) × ( 5.25 )2

= 2 × \(\displaystyle \frac{{22}}{7}\) × 27.5625

= \(\displaystyle \frac{{44}}{7}\) × 27.5625

= \(\displaystyle \frac{{1212.75}}{7}\) 

= 173.25 cm2

Now, Cost of tin-plating at the rate Rs 16 per 100 cm2

Cost of tin-plating 173.25 cm2 area = Rs 173.25 × \(\displaystyle \frac{{16}}{{100}}\)

= Rs \(\displaystyle \frac{{2772}}{{100}}\)

= Rs 27.72

∴ The cost of tin-plating inside at the rate of Rs 16 per 100 cm2 = Rs 27.72 .

Q6. Find the radius of a sphere whose surface area is 154 cm2.

Solution :

According to the question,

Given, Surface area of a sphere = 154 cm2

So, Surface area of a sphere = 4πr2

⇒ 154 = 4 × \(\displaystyle \frac{{22}}{7}\) × r2

⇒ 154 = \(\displaystyle \frac{{88}}{7}\) × r2

⇒ 154 × 7 = 88r2

⇒ 1078 = 88r20

⇒

=r2

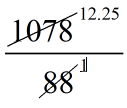
⇒ √12.25 = r2                     [ if you not understand than, using long division method ]

⇒ 3.5 cm2 = r

∴ The radius of a sphere = 3.5 cm2 .

Q7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.

Solution :

According to the question,

Given, \(\displaystyle {{d}_{m}}\) = \(\displaystyle \frac{1}{4}{{d}_{e}}\)

\(\displaystyle {{r}_{m}}\) = \(\displaystyle \frac{1}{4}{{r}_{e}}\)

So, \(\displaystyle {{r}_{m}}\) = \(\displaystyle \frac{1}{4}{{r}_{e}}\)

⇒ 4\(\displaystyle {{r}_{m}}\) = \(\displaystyle {{r}_{e}}\)

Now, \(\displaystyle \frac{{surface\,area\,of\,the\,moon\,}}{{surface\,area\,of\,the\,earth\,}}\,=\,\frac{{4\pi {{r}_{m}}^{2}}}{{4\pi {{r}_{e}}^{2}}}\)

=

= \(\displaystyle \frac{{{{r}_{m}}^{2}}}{{{{r}_{e}}^{2}}}\)

= \(\displaystyle \frac{{{{r}_{m}}^{2}}}{{{{{(4{{r}_{m}})}}^{2}}}}\)

= \(\displaystyle \frac{{{{r}_{m}}^{2}}}{{16{{r}_{m}}^{2}}}\)

=

= \(\displaystyle \frac{1}{{16}}\)

∴ The ratio of their surface areas = 1 : 16 .

Q8. A hemisphere bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.

Solution :

According to the question,

Given, Inner radius = 5 cm

thick = 0.25

Now, The outer radius of hemisphere = 5 + 0.25

= 5.25 cm

So, Curved surface area of the bowl = 2πr2

= 2 × \(\displaystyle \frac{{22}}{7}\) × ( 5.25 )2 

= 2 × \(\displaystyle \frac{{22}}{7}\) × 27.5625

= \(\displaystyle \frac{{44}}{7}\) × 27.5625

= \(\displaystyle \frac{{1212.75}}{7}\) 

= 173.25 cm2

∴ The curved surface area of the bowl = 173.25 cm2 .

Q9. A right circular cylinder just enclosed a sphere of radius r ( see fig. 13.22 ). Find

(i) surface area of the sphere

(ii) curved surface area of the cylinder,

(iii) ratio of the area obtained in (i) and (ii).

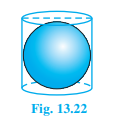
Solution :

According to the given '' right circular cylinder ''

Given, Radius = r

(i) surface area of the sphere = 4πr2

(ii) curved surface area of the cylinder = 2πrh = 2πr( 2r )                   [ Because, Height is twice of radius ]

= 4πr2

(iii) ratio of the area obtained in (i) and (ii) = \(\displaystyle \frac{{surface\,area\,of\,the\,sphere}}{{curved\,surface\,area\,of\,the\,cylinder}}\)

= \(\displaystyle \frac{{4\pi {{r}^{2}}}}{{4\pi {{r}^{2}}}}\)

=

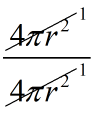
= \(\displaystyle \frac{1}{1}\)

∴ Ratio of the area obtained = 1:1 .

 

Class 9 Maths Chapter 13 Surface Area And Volume :

Leave a Comment

Your email address will not be published. Required fields are marked *

The maximum upload file size: 256 MB. You can upload: image, audio, video, document, spreadsheet, interactive, text, archive, code, other. Links to YouTube, Facebook, Twitter and other services inserted in the comment text will be automatically embedded. Drop file here