NCERT Solutions Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.2
Introduction:
In this exercise 9.2 of chapter 9 Perimeter and Area, we will get to know about the circle, that how to find the circumference, radius, area and diameter of circle. As we know that distance around the circular region is known as its Circumference.
NCERT Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.1
NCERT Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.2
Class 7 Maths Exercise 9.2 (Page-158)
Q1. Find the circumference of the circles with the following radius. (Take π = \(\displaystyle \frac{{22}}{7}\) )
(a) 14 cm
(b) 28 mm
(c) 21 cm
Solution:
a) Circumference of Circle = 2 πr
= 2 × \(\displaystyle \frac{{22}}{7}\) × 14
= 2 × 22 × 2
= 44 × 2
= 88cm.
b) Circumference of Circle = 2 πr
= 2 × \(\displaystyle \frac{{22}}{7}\) × 28
= 2 × 22 × 4
= 44 × 4
= 176mm
c) Circumference of Circle = 2 πr
= 2 × \(\displaystyle \frac{{22}}{7}\) × 21
= 2 × 22 × 3
= 44 × 3
= 132cm.
Q2. Find the area of the following circles, given that (Take π = \(\displaystyle \frac{{22}}{7}\) )
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm
Solution:
a) Area of Circle = πr²
= \(\displaystyle \frac{{22}}{7}\) × 14 × 14
=22 × 2 × 14
= 44× 14
= 616mm²
b) here diameter is 49m, so radius will be \(\displaystyle \frac{{diameter}}{2}\) i.e 24.5m
Area of Circle = πr²
= \(\displaystyle \frac{{22}}{7}\) × 24.5 × 24.5
=22 × 3.5× 24.5
= 77 × 24.5
= 1886.5m²
c) Area of Circle = πr²
= \(\displaystyle \frac{{22}}{7}\) × 5 × 5
= \(\displaystyle \frac{{22}}{7}\) × 25
= \(\displaystyle \frac{{22 × 25}}{7}\)
= \(\displaystyle \frac{{550}}{7}\)
= 78.5cm²
Q3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π = \(\displaystyle \frac{{22}}{7}\) )
Solution:
Circumference of Circle = 2 πr
154 = 2 × \(\displaystyle \frac{{22}}{7}\) × r
\(\displaystyle \frac{{154 × 7}}{22}\) = 2r
7 × 7= 2r
49 = 2r
r = \(\displaystyle \frac{{49}}{2}\)
r = 24.5m.
Now,
Area of Circle = πr²
= \(\displaystyle \frac{{22}}{7}\) × 24.5 × 24.5
=22 × 3.5× 24.5
= 77 × 24.5
= 1886.5m²
Q4. A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs ₹ 4 per metre. (Take π = \(\displaystyle \frac{{22}}{7}\) )
Solution: here diameter is 21m, so radius will be \(\displaystyle \frac{{diameter}}{2}\) i.e 10.5m
Circumference of Circle = 2 πr
= 2 × \(\displaystyle \frac{{22}}{7}\) × 10.5
= 2 × 22 × 1.5
= 44 × 1.5
= 66m.
If he makes 2 rounds of fence then we multiply circumference with 2
= 66 × 2
= 132m.
So, the length of rope is 132m.
Now, if the cost of 1m rope is ₹ 4, then cost of 132m rope will be = 132× 4
= 528
So, the cost of 132m rope is ₹ 528.
Q5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14).

Solution:
Given: the radius of circular sheet(R) = 4cm
radius of small circle (r) = 3cm
Area of remaining sheet = Area of sheet - Area of small circle
= πR² - πr²
= π ( R² -r²)( taking π as common)
= 3.14 ( 4² - 3²)
= 3.14 (16- 9)
= 3.14 (7)
= 21.98
Hence, the area of remaining sheet is 21.98cm².
Q6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one metre of the lace costs ₹ 15. (Take π = 3.14).
Solution: here diameter is 1.5m, so radius will be \(\displaystyle \frac{{diameter}}{2}\) i.e \(\displaystyle \frac{{1.5}}{2}\)m
Circumference of Circle = 2 πr
= 2 × 3.14 × \(\displaystyle \frac{{1.5}}{2}\)
= 3.14 × 1.5
= 4.71m
If the cost of 1m lace is ₹ 15, then cost of 4.71m lace will be = 15 × 4.71
= 70.65
Hence, the cost of lace is ₹ 70.65,
Q7. Find the perimeter of the given figure, which is a semicircle including its diameter.
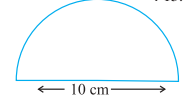
Solution: Perimeter of given Figure = Circumference of semi-circle + Diameter
= πr + D
= \(\displaystyle \frac{{22}}{7}\) × 5 + 10
= \(\displaystyle \frac{{110}}{7}\) + 10
= \(\displaystyle \frac{{110 × 1}}{7 × 1}\) + \(\displaystyle \frac{{10 × 7}}{1 × 7}\)
= \(\displaystyle \frac{{110 + 70}}{7}\)
= \(\displaystyle \frac{{180}}{7}\)
= 25.71
So, the perimeter of given figure is 25.71 cm.
Q8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/ m².(Take π = 3.14).
Solution: here diameter is 1.6m, so radius will be \(\displaystyle \frac{{diameter}}{2}\) i.e 0.8m
Area of Circle = πr²
= 3.14 × 0.8 × 0.8
= 3.14 × 0.64
= 2.0096m²
if the rate of polishing is ₹ 15/ m², then rate of polishing 2.0096m² = 2.0096 × 15
= 30.1440
So, the rate of polishing 2.0096m² is ₹ 30.1440.
Q9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = \(\displaystyle \frac{{22}}{7}\) )
Solution: Circumference of circle = 2 πr
44 = 2 × \(\displaystyle \frac{{22}}{7}\) × r
\(\displaystyle \frac{{44 × 7}}{22}\) = 2r
r = \(\displaystyle \frac{{2× 7 }}{2}\)
r = 7
So, the radius of circle is 7cm.
Area of Circle = πr²
= \(\displaystyle \frac{{22}}{7}\) × 7 × 7
= 22× 7
= 154
Hence, the area of circle is 154 cm²
now, the same wire is used then the perimeter will be same as length of wire
Perimeter of square = 4 × side
44 = 4 × side
side =\(\displaystyle \frac{{44}}{4}\)
side = 11cm
So, the side of square is 11 cm .
Area of Square = side × side
= 11 × 11
= 121 cm²
hence the area of circle is more, so it will enclose more area.
Q10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed, (as shown in the given figure below). Find the area of the remaining sheet. (Take π = \(\displaystyle \frac{{22}}{7}\) )

Solution: Area of remaining sheet = Area of circular card -Area of 2 circles + area of rectangle
= πr² - 2 ×(πr²) + l × b
=( \(\displaystyle \frac{{22}}{7}\) × 14 × 14) - ( 2 × \(\displaystyle \frac{{22}}{7}\) × 3.5 × 3.5 + 3×1)
= (22 × 2 × 14) - ( 2 × 22 × 0.5 ×3.5 + 3)
= ( 44 × 14) - ( 2 × 11 ×3.5 +3)
= 616 - (77 +3)
= 616 - 80
= 536
Hence, the area of remaining sheet is 536 cm².
Q11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution: Area of leftover aluminium sheet = Area of sheet - Area of circle
= side × side - πr²
= (6 × 6 ) - (3.14 × 2 × 2)
= 36 - (3.44 × 4)
= 36 - 12.56
= 23.44
Hence the area of remaining aluminium sheet is 23.44 cm²
Q12. The circumference of a circle is 31.4 cm. Find the radius and the area of the circle. (Take π = 3.14)
Solution: Circumference of Circle = 2 πr
31.4 = 2 × 3.14 × r
\(\displaystyle \frac{{31.4}}{3.14}\) ) = 2 × r
2r = \(\displaystyle \frac{{314 × 100}}{314 × 10}\) )
2r = 10
r = \(\displaystyle \frac{{10}}{2}\) )
r = 5
So, the radius of circle is 5 cm.
now,
Area of Circle = πr²
= 3.14 × 5 × 5
= 3.14 × 25
= 78.5
Hence the area of circle is 78.5 cm².
Q13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take π = 3.14)
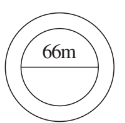
Solution:
Given : radius of Flower bed (r) = 33m
radius of Outer circle = 33 + 4 = 37 m
Area of path = Area of outer circle - Area of flower bed
= πR² - πr²
= π ( R² - r²) ( taking π common)
= 3.14 (37² - 33²)
= 3.14 ( 1369 - 1089)
= 3.14 ×280
= 879.2
Hence, the area of this path is 879.2 m².
Q14. A circular flower garden has an area of 314 m². A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler can water the entire garden?[Take π = 3.14]
Solution: Area of Sprinkler = πr²
= 3.14 × 12 × 12
= 3.14 × 144
= 452.16 m².
Hence the area of sprinkler is more than the area of garden. So, the Sprinker can water the entire garden.
Q15. Find the circumference of the inner and the outer circles, shown in the given figure. (Take π = 3.14)
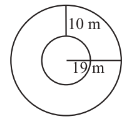
Solution: Circumference of Outer circle = 2πr
= 2 × 3.14 × 19
= 3.14 × 38
= 119.32m
Circumference of Inner Circle = 2πr
= 2 × 3.14 × 9 ( to find radius we will subtract the path from outer radius)
= 3.14 × 18
= 56.52m
Hence the circumference of outer circle is 119.32m and circumference of inner circle is 56.52m.
Q16. How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = \(\displaystyle \frac{{22}}{7}\) )
Solution: Let the number of rotation be n
distance covered = n × circumference of wheel
35200cm = n × 2πr (convert 352m into cm)
35200 = n × 2 × \(\displaystyle \frac{{22}}{7}\) × 28
35200 = 2n × 22 × 4
35200 = 2n × 88
\(\displaystyle \frac{{35200}}{88}\) = 2n
400 = 2n
n = \(\displaystyle \frac{{400}}{2}\)
n = 200
Hence, the wheel will rotate 200 times to go to 352m.
Q17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution: Circumference of circle = 2πr
= 2 × 3.14× 15
= 3.4× 30
= 94.2
So, the tip of the minute hand will move 94.2 cm in 1 hour.