NCERT Solutions Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.1
Introduction:
In this exercise 9.1 of chapter Area and Perimeter, we will learn about how to find the area, height and base of shapes other than square and rectangle like parallelogram , triangle. By using certain formulas given in this chapter we will solve the following Questions.
NCERT Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.1
NCERT Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.2
Class 7 Maths Exercise 9.1 (Page-151)
Q1. Find the area of each of the following parallelograms:
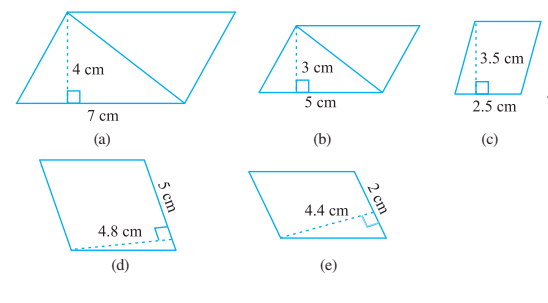
Solutions:
a) Given: Base = 7cm
Height = 4cm
So, the area of Parallelogram = base × height
= 7 × 4
= 28 cm²
b) Given: Base = 5cm
Height = 3cm
So, the area of Parallelogram = base × height
= 5 × 3
= 15 cm²
c) Given: Base = 2.5cm
Height = 3.5cm
So, the area of Parallelogram = base × height
= 2.5 × 3.5
= 8.75 cm²
d) Given: Base = 5cm
Height = 4.8cm
So, the area of Parallelogram = base × height
= 5 × 4.8
= 24 cm²
e) Given: Base = 2cm
Height = 4.4cm
So, the area of Parallelogram = base × height
= 2 × 4.4
= 8.8 cm²
Q2. Find the area of each of the following triangles:
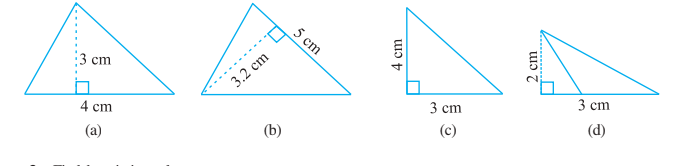
Solutions:
a) Given: Base = 7cm
Height = 4cm
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × 4 × 3
= \(\displaystyle \frac{{12}}{2}\)
= 6 cm²
b) Given: Base = 5cm
Height = 3.2cm
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × 5 × 3.2
= \(\displaystyle \frac{{16}}{2}\)
= 8 cm²
c) Given: Base = 3cm
Height = 4cm
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × 3 × 4
= \(\displaystyle \frac{{12}}{2}\)
= 6 cm²
d) Given: Base = 3cm
Height = 2cm
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × 3 × 2
= \(\displaystyle \frac{{6}}{2}\)
= 3 cm²
Q3. Find the missing values:
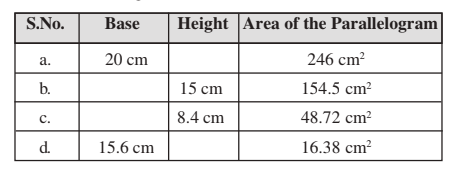
Solutions:
a)
Given: Base = 20 cm
Area of Parallelogram = 246cm²
So, the area of Parallelogram = base × height
246 = 20 × h
h = \(\displaystyle \frac{{246}}{20}\)
= 12.3 cm
b)
Given: height = 15 cm
Area of Parallelogram = 154.5 cm²
So, the area of Parallelogram = base × height
154.5 cm² = base × 15
base = \(\displaystyle \frac{{154.5}}{15}\)
base = 10.3 cm
c)
Given: height = 8.4 cm
Area of Parallelogram = 48.72 cm²
So, the area of Parallelogram = base × height
48.72 cm² = base × 8.4
base = \(\displaystyle \frac{{48.72}}{8.4}\)
base = 5.8 cm
d)
Given: Base = 15.6 cm
Area of Parallelogram = 16.38cm²
So, the area of Parallelogram = base × height
16.38 = 15.6 × h
h = \(\displaystyle \frac{{16.38}}{15.6}\)
= 1.05 cm
Q4. Find the missing values:

Solutions:
a)
Given: Base = 15cm
Area of Triangle = 87 cm²
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
87 = \(\displaystyle \frac{{1}}{2}\) × 15 × h
87 × 2= 15 × h
h = \(\displaystyle \frac{{174}}{15}\)
= 11.6 cm
b)
Given: height = 31.4 mm
Area of Triangle = 1256 mm²
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
1256 = \(\displaystyle \frac{{1}}{2}\) × b × 31.4
1256 × 2 = 31.4× b
b = \(\displaystyle \frac{{2512}}{31.4}\)
= 80 mm
c)
Given: Base = 22cm
Area of Triangle = 170.5 cm²
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
170.5 = \(\displaystyle \frac{{1}}{2}\) × 22 × h
170.5 × 2 = 22 × h
h = \(\displaystyle \frac{{341}}{22}\)
= 15.5 cm
Q5. PQRS is a parallelogram(fig 9.14). QM is the height of Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
a) the area of the parallelogram PQRS
b) QN, if PS = 8 cm
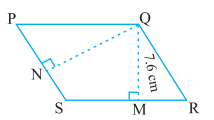
Solution:
a)
Given: SR (Base) = 12cm
QM (Height) = 7.6cm
So, the area of Parallelogram = base × height
= 12 × 7.6
= 91.2 cm²
So, the area of parallelogram PQRS is 91.2 cm² .
b)
Given: PS (Base) = 8cm
To Find : QN (height)
Area of parallelogram = 91.2 cm²
So, the area of Parallelogram = base × height
91.2 = 8 × h
h = \(\displaystyle \frac{{91.2}}{8}\)
h = 11.4 cm
So, the QN is 11.4 cm
Q6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (fig 9.15). If the area of the parallelogram is 1470 cm², AB = 35 cm and AD = 49 cm, find the length of BM and DL.

Solutions:
Given :
Area of parallelogram = 1470 cm²
AB = 35 cm
AD = 49 cm
the area of Parallelogram = base × height
1470 = AB × DL
1470 = 35 × DL
DL = \(\displaystyle \frac{{1470}}{35}\)
DL = 42cm
the area of Parallelogram = base × height
1470 = DA × BM
1470 = 49 × BM
DL = \(\displaystyle \frac{{1470}}{49}\)
DL = 30 cm
So, the length of BM is 30 cm and DL is 42 cm.
Q7. ∆ABC is right angled at A (fig 9.16). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD.
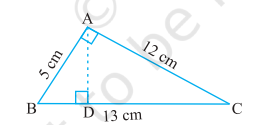
Solutions: ATQ , given triangle is right angle. so, AB will be the base and AC will be the height.
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × AB × AC
= \(\displaystyle \frac{{1}}{2}\) × 5 × 12
= \(\displaystyle \frac{{1}}{2}\) × 60
= 30 cm²
So, the area of ΔABC is 30 cm²
the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
30 = \(\displaystyle \frac{{1}}{2}\) × BC × AD
30 = \(\displaystyle \frac{{1}}{2}\) × 13 × AD
AD = \(\displaystyle \frac{{30 × 2}}{13}\)
AD = \(\displaystyle \frac{{60}}{13}\)
Hence, the length of AD is \(\displaystyle \frac{{60}}{13}\) cm.
Q8. ∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (fig 9.17). The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?

Solution: In ΔABC, AD(height) is 6cm and BC ( base) is 9cm.
So, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
= \(\displaystyle \frac{{1}}{2}\) × BC × AD
= \(\displaystyle \frac{{1}}{2}\) × 9 × 6
= \(\displaystyle \frac{{1}}{2}\) × 54
= \(\displaystyle \frac{{54}}{2}\)
= 27cm² .
Now, the area of Triangle = \(\displaystyle \frac{{1}}{2}\) × base × height
27 = \(\displaystyle \frac{{1}}{2}\) × AB × CE
27 = \(\displaystyle \frac{{1}}{2}\) × 7.5 × CE
CE= \(\displaystyle \frac{{27 × 2}}{7.5}\)
CE = \(\displaystyle \frac{{54}}{7.5}\)
CE = 7.2cm
Hene the area of ∆ABC is 27cm² and the height from C to AB i.e., CE is 7.2cm.