NCERT Solutions Class 7 Maths Chapter 8 Rational Numbers Exercise 8.1
Introduction:
A number that can be expressed in the form \(\displaystyle \frac{{p}}{q}\) , where p and q are integers and q≠ 0, is called a rational number. All integers and fractions are rational numbers. Rational numbers are classified as positive and negative rational numbers. When the numerator and denominator both are positive integers, it is a positive rational number. When either the numerator or the denominator is a negative integer, it is a negative rational number.
NCERT Class 7 Maths Chapter 8 Rational Number Exercise 8.1
NCERT Class 7 Maths Chapter 8 Rational Number Exercise 8.2
Class 7 Maths Exercise 8.1 (Page-133)
Q1. List five rational numbers between:
(i) -1 and 0
(ii) -2 and -1
(iii) \(\displaystyle \frac{{-4}}{5}\) and \(\displaystyle \frac{{-2}}{3}\)
(iv) \(\displaystyle \frac{{-1}}{2}\) and \(\displaystyle \frac{{2}}{3}\)
Solution:
(i) To find the numbers, first we will make the given rational.
\(\displaystyle \frac{{-1}}{1}\) and \(\displaystyle \frac{{0}}{1}\)
Now, to make the denominator 6, we have to multiply it with the denominator.
\(\displaystyle \frac{{-1 ×6}}{1 × 6}\) and \(\displaystyle \frac{{0 × 6}}{1× 6}\)
\(\displaystyle \frac{{-6}}{6}\) and \(\displaystyle \frac{{0}}{6}\)
Now, we will write the 5 rational number between \(\displaystyle \frac{{-6}}{6}\) and \(\displaystyle \frac{{0}}{6}\)
\(\displaystyle \frac{{-5}}{6}\), \(\displaystyle \frac{{-4}}{6}\), \(\displaystyle \frac{{-3}}{6}\), \(\displaystyle \frac{{-2}}{6}\), \(\displaystyle \frac{{-1}}{6}\)
(ii) To find the numbers, first we will make the given rational.
\(\displaystyle \frac{{-2}}{1}\) and \(\displaystyle \frac{{1}}{1}\)
Now, to make the denominator 6, we have to multiply it with the denominator.
\(\displaystyle \frac{{-2 ×6}}{1 × 6}\) and \(\displaystyle \frac{{1 × 6}}{1× 6}\)
\(\displaystyle \frac{{-12}}{6}\) and \(\displaystyle \frac{{6}}{6}\)
Now, we will write the 5 rational number between \(\displaystyle \frac{{-6}}{6}\) and \(\displaystyle \frac{{0}}{6}\)
\(\displaystyle \frac{{-11}}{6}\), \(\displaystyle \frac{{-10}}{6}\), \(\displaystyle \frac{{-9}}{6}\), \(\displaystyle \frac{{-8}}{6}\), \(\displaystyle \frac{{-7}}{6}\)
(iii) to find the rational number given number we have to make the denominator same. so we will take 45 as common number for both to make denominator same because if we take 15 or 30, we will unable to find 5 rational number.
\(\displaystyle \frac{{-4 ×9}}{5 × 9}\) and \(\displaystyle \frac{{-2 × 15}}{3× 15}\)
\(\displaystyle \frac{{-36}}{45}\) and \(\displaystyle \frac{{-30}}{45}\)
Now, we will write the 5 rational number between \(\displaystyle \frac{{-36}}{45}\) and \(\displaystyle \frac{{- 30}}{45}\)
\(\displaystyle \frac{{-35}}{45}\), \(\displaystyle \frac{{-34}}{45}\), \(\displaystyle \frac{{-33}}{45}\), \(\displaystyle \frac{{-32}}{45}\), \(\displaystyle \frac{{-31}}{45}\)
(iv) to find the rational number given number we have to make the denominator same.
\(\displaystyle \frac{{-1×3}}{2×3}\) and \(\displaystyle \frac{{2×2}}{3×2}\)
\(\displaystyle \frac{{-3}}{6}\) and \(\displaystyle \frac{{4}}{6}\)
Now, we will write the 5 rational number between \(\displaystyle \frac{{-3}}{6}\) and \(\displaystyle \frac{{4}}{6}\)
\(\displaystyle \frac{{-2}}{6}\), \(\displaystyle \frac{{-1}}{6}\), \(\displaystyle \frac{{1}}{6}\), \(\displaystyle \frac{{2}}{6}\), \(\displaystyle \frac{{3}}{6}\)
Q2. Write four rational numbers in each of the following patterns:
(i) \(\displaystyle \frac{{-3}}{5}\) , \(\displaystyle \frac{{-6}}{10}\) , \(\displaystyle \frac{{-9}}{15}\) , \(\displaystyle \frac{{-12}}{20}\) , ......
(ii) \(\displaystyle \frac{{-1}}{4}\) , \(\displaystyle \frac{{-2}}{8}\) , \(\displaystyle \frac{{-3}}{12}\) , ......
(iii) \(\displaystyle \frac{{-1}}{6}\) , \(\displaystyle \frac{{2}}{-12}\) , \(\displaystyle \frac{{3}}{-18}\) , \(\displaystyle \frac{{4}}{-24}\) ,......
(iv) \(\displaystyle \frac{{-2}}{3}\), \(\displaystyle \frac{{2}}{-3}\) , \(\displaystyle \frac{{4}}{-6}\) , \(\displaystyle \frac{{6}}{-9}\) , .....
Solution:
(i) Given pattern is → \(\displaystyle \frac{{-3×1}}{5×1}\), \(\displaystyle \frac{{-3×2}}{5×2}\), \(\displaystyle \frac{{-3×3}}{5×3}\), \(\displaystyle \frac{{-3×4}}{5×4}\),
According to this pattern, the four more rationals are:
\(\displaystyle \frac{{-3×5}}{5×5}\), \(\displaystyle \frac{{-3×6}}{5×6}\), \(\displaystyle \frac{{-3×7}}{5×7}\), \(\displaystyle \frac{{-3×8}}{5×8}\),
= \(\displaystyle \frac{{-15}}{25}\), \(\displaystyle \frac{{-18}}{30}\), \(\displaystyle \frac{{-21}}{35}\) and \(\displaystyle \frac{{-24}}{40}\)
(ii)
Given pattern is → \(\displaystyle \frac{{-1×1}}{4×1}\), \(\displaystyle \frac{{-1×2}}{4×2}\), \(\displaystyle \frac{{-1×3}}{4×3}\)
According to this pattern, the four more rationals are:
, \(\displaystyle \frac{{-1×4}}{4×4}\), ,\(\displaystyle \frac{{-1×5}}{4×5}\), \(\displaystyle \frac{{-1×6}}{4×6}\), \(\displaystyle \frac{{-1×7}}{4×7}\)
= \(\displaystyle \frac{{-4}}{16}\), \(\displaystyle \frac{{-5}}{20}\), \(\displaystyle \frac{{-6}}{24}\) and \(\displaystyle \frac{{-7}}{28}\)
(iii)
Given pattern is → \(\displaystyle \frac{{-1×1}}{6×1}\), \(\displaystyle \frac{{1×2}}{-6×2}\), \(\displaystyle \frac{{1×3}}{-6×3}\), \(\displaystyle \frac{{1×4}}{-6×4}\)
According to this pattern, the four more rationals are:
\(\displaystyle \frac{{1×5}}{-6×5}\), \(\displaystyle \frac{{1×6}}{-6×6}\), \(\displaystyle \frac{{1×7}}{-6×7}\), \(\displaystyle \frac{{1×8}}{-6×8}\),
= \(\displaystyle \frac{{5}}{-30}\), \(\displaystyle \frac{{6}}{-36}\), \(\displaystyle \frac{{7}}{-42}\) and \(\displaystyle \frac{{8}}{-48}\)
(iv)
Given pattern is → \(\displaystyle \frac{{-2×1}}{3×1}\), \(\displaystyle \frac{{2×1}}{-3×1}\), \(\displaystyle \frac{{2×2}}{-3×2}\), \(\displaystyle \frac{{2×3}}{-3×3}\)
According to this pattern, the four more rationals are:
\(\displaystyle \frac{{2×4}}{-3×4}\), \(\displaystyle \frac{{2×5}}{-3×5}\), \(\displaystyle \frac{{2×6}}{-3×6}\) , \(\displaystyle \frac{{2×7}}{-3×7}\) ,
= \(\displaystyle \frac{{8}}{-12}\), \(\displaystyle \frac{{10}}{-15}\), \(\displaystyle \frac{{12}}{-18}\) and \(\displaystyle \frac{{14}}{-21}\)
Q3. Give four more rational numbers equivalent to:
(i) \(\displaystyle \frac{{-2}}{7}\)
(ii) \(\displaystyle \frac{{5}}{-3}\)
(iii) \(\displaystyle \frac{{4}}{9}\)
Solution:
(i) \(\displaystyle \frac{{-2}}{7}\) = \(\displaystyle \frac{{-2×2}}{7×2}\) = \(\displaystyle \frac{{-4}}{14}\)
\(\displaystyle \frac{{-2}}{7}\) = \(\displaystyle \frac{{-2×3}}{7×3}\) = \(\displaystyle \frac{{-6}}{21}\)
\(\displaystyle \frac{{-2}}{7}\) = \(\displaystyle \frac{{-2×4}}{7×4}\) = \(\displaystyle \frac{{-8}}{28}\)
\(\displaystyle \frac{{-2}}{7}\) = \(\displaystyle \frac{{-2×5}}{7×5}\) = \(\displaystyle \frac{{-10}}{35}\)
Hence the four rational number equivalent to \(\displaystyle \frac{{-2}}{7}\) are : \(\displaystyle \frac{{-4}}{14}\), \(\displaystyle \frac{{-6}}{21}\), \(\displaystyle \frac{{-8}}{28}\) and \(\displaystyle \frac{{-10}}{35}\)
(ii) \(\displaystyle \frac{{5}}{-3}\) = \(\displaystyle \frac{{5×2}}{-3×2}\) = \(\displaystyle \frac{{10}}{-6}\)
\(\displaystyle \frac{{5}}{-3}\) = \(\displaystyle \frac{{5×3}}{-3×3}\) = \(\displaystyle \frac{{15}}{-9}\)
\(\displaystyle \frac{{5}}{-3}\) = \(\displaystyle \frac{{5×4}}{-3×4}\) = \(\displaystyle \frac{{20}}{-12}\)
\(\displaystyle \frac{{5}}{-3}\) = \(\displaystyle \frac{{5×5}}{-3×5}\) = \(\displaystyle \frac{{25}}{-15}\)
Hence the four rational number equivalent to \(\displaystyle \frac{{5}}{-3}\) are : \(\displaystyle \frac{{10}}{-6}\) , \(\displaystyle \frac{{15}}{-9}\) , \(\displaystyle \frac{{20}}{-12}\) and \(\displaystyle \frac{{25}}{-15}\)
(iii) \(\displaystyle \frac{{4}}{9}\)= \(\displaystyle \frac{{4×2}}{9×2}\) = \(\displaystyle \frac{{8}}{18}\)
\(\displaystyle \frac{{4}}{9}\)= \(\displaystyle \frac{{4×3}}{9×3}\) = \(\displaystyle \frac{{12}}{27}\)
\(\displaystyle \frac{{4}}{9}\)= \(\displaystyle \frac{{4×4}}{9×4}\) = \(\displaystyle \frac{{16}}{36}\)
\(\displaystyle \frac{{4}}{9}\)= \(\displaystyle \frac{{4×5}}{9×5}\) = \(\displaystyle \frac{{20}}{45}\)
Hence the four rational number equivalent to \(\displaystyle \frac{{4}}{9}\) = \(\displaystyle \frac{{8}}{18}\), \(\displaystyle \frac{{12}}{27}\), \(\displaystyle \frac{{16}}{36}\) and \(\displaystyle \frac{{20}}{45}\)
Q4. Draw the number line and represent the following rational numbers on it:
(i) \(\displaystyle \frac{{3}}{4}\)
(ii) \(\displaystyle \frac{{-5}}{8}\)
(iii) \(\displaystyle \frac{{-7}}{4}\)
(iv) \(\displaystyle \frac{{7}}{8}\)
Solution:
(i) 
(ii) 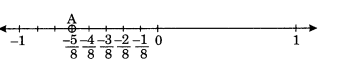
(iii) 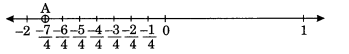
(iv) 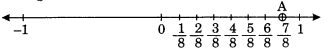
Q5. The points P,Q,R,S,T,U,A and B on the number line are such that, TR=RS=SU and AP=PQ=QB. Name the rational numbers represented by P,Q.R and S.

Solution: we will take denominator 3
So, P = \(\displaystyle \frac{{7}}{3}\)
Q = \(\displaystyle \frac{{8}}{3}\)
R = \(\displaystyle \frac{{-4}}{3}\)
S = \(\displaystyle \frac{{-5}}{3}\)
Q6. Which of the following pairs represent the same rational number?
(i) \(\displaystyle \frac{{-7}}{21}\) and \(\displaystyle \frac{{3}}{9}\)
(ii) \(\displaystyle \frac{{-16}}{20}\) and \(\displaystyle \frac{{20}}{-25}\)
(iii) \(\displaystyle \frac{{-2}}{-3}\) and \(\displaystyle \frac{{2}}{3}\)
(iv) \(\displaystyle \frac{{-3}}{5}\) and \(\displaystyle \frac{{-12}}{20}\)
(v) \(\displaystyle \frac{{8}}{-5}\) and \(\displaystyle \frac{{-24}}{15}\)
(vi) \(\displaystyle \frac{{1}}{3}\) and \(\displaystyle \frac{{-1}}{9}\)
(vii) \(\displaystyle \frac{{-5}}{-9}\) and \(\displaystyle \frac{{5}}{-9}\)
Solution:
(i) \(\displaystyle \frac{{-7}}{21}\) = \(\displaystyle \frac{{-1}}{3}\) and \(\displaystyle \frac{{3}}{9}\) = \(\displaystyle \frac{{1}}{3}\)
\(\displaystyle \frac{{-1}}{3}\) ≠ \(\displaystyle \frac{{1}}{3}\)
(ii) \(\displaystyle \frac{{-16}}{20}\) = \(\displaystyle \frac{{-4}}{5}\) and \(\displaystyle \frac{{20}}{-25}\) = \(\displaystyle \frac{{4}}{-5}\)
\(\displaystyle \frac{{-4}}{5}\) = \(\displaystyle \frac{{4}}{-5}\)
(iii) \(\displaystyle \frac{{-2}}{-3}\) = \(\displaystyle \frac{{2}}{3}\) and \(\displaystyle \frac{{2}}{3}\)
\(\displaystyle \frac{{2}}{3}\) = \(\displaystyle \frac{{2}}{3}\)
(iv) \(\displaystyle \frac{{-3}}{5}\)
\(\displaystyle \frac{{-12}}{20}\)= \(\displaystyle \frac{{-3}}{5}\)
\(\displaystyle \frac{{-3}}{5}\) = \(\displaystyle \frac{{-3}}{5}\)
(v) \(\displaystyle \frac{{8}}{-5}\)
\(\displaystyle \frac{{-24}}{15}\) = \(\displaystyle \frac{{-8}}{5}\)
\(\displaystyle \frac{{8}}{-5}\) = \(\displaystyle \frac{{-8}}{5}\)
(vi) \(\displaystyle \frac{{1}}{3}\) ≠ \(\displaystyle \frac{{-1}}{9}\)
(vii) \(\displaystyle \frac{{-5}}{-9}\) = \(\displaystyle \frac{{5}}{9}\)
\(\displaystyle \frac{{5}}{9}\) and \(\displaystyle \frac{{5}}{-9}\)
\(\displaystyle \frac{{5}}{9}\) ≠ \(\displaystyle \frac{{5}}{-9}\)
Q7. Rewrite the following rational numbers in the simplest form:
(i) \(\displaystyle \frac{{-8}}{6}\)
(ii) \(\displaystyle \frac{{25}}{45}\)
(iii) \(\displaystyle \frac{{-44}}{72}\)
(iv) \(\displaystyle \frac{{-8}}{10}\)
Solution:
(i) \(\displaystyle \frac{{-8}}{6}\) = \(\displaystyle \frac{{-4}}{3}\) ( dividing by 2)
(ii) \(\displaystyle \frac{{25}}{45}\) = \(\displaystyle \frac{{5}}{9}\) (dividing by 5)
(iii) \(\displaystyle \frac{{-44}}{72}\) = \(\displaystyle \frac{{-11}}{18}\) ( dividing by 4)
(iv) \(\displaystyle \frac{{-8}}{10}\) = \(\displaystyle \frac{{-4}}{5}\) ( dividing by 2)
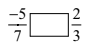
Q8. Fill in the boxes with the correct symbol out of >,< and =
(1) 
(ii) ![]()
(iii) 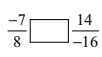
(iv) ![]()
(v) 
(vi) ![]()
(vii) 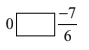
Solution:
(i) \(\displaystyle \frac{{-5}}{7}\) < \(\displaystyle \frac{{2}}{3}\) (ii) \(\displaystyle \frac{{-4}}{5}\) < \(\displaystyle \frac{{-5}}{7}\) Taking L.C.M to make denominator same \(\displaystyle \frac{{-4×7}}{5×7}\) , \(\displaystyle \frac{{-5×5}}{7×5}\) \(\displaystyle \frac{{-28}}{35}\) , \(\displaystyle \frac{{-25}}{35}\) \(\displaystyle \frac{{-28}}{35}\) < \(\displaystyle \frac{{-25}}{35}\) (iii) \(\displaystyle \frac{{-7}}{8}\) , \(\displaystyle \frac{{-14}}{16}\)
dividing \(\displaystyle \frac{{-14}}{16}\) by 2 = \(\displaystyle \frac{{7}}{-8}\)
\(\displaystyle \frac{{-7}}{8}\) = \(\displaystyle \frac{{7}}{-8}\)
(iv) Taking L.C.M to make denominator same
\(\displaystyle \frac{{-8×4}}{5×4}\) , \(\displaystyle \frac{{-7×5}}{4×5}\)
\(\displaystyle \frac{{-32}}{20}\) , \(\displaystyle \frac{{-35}}{20}\)
\(\displaystyle \frac{{-32}}{20}\) > \(\displaystyle \frac{{-35}}{20}\)
(v) Taking L.C.M to make denominator same
\(\displaystyle \frac{{1×4}}{-3×4}\) , \(\displaystyle \frac{{-1×3}}{4×3}\)
\(\displaystyle \frac{{4}}{-12}\) , \(\displaystyle \frac{{-3}}{12}\)
\(\displaystyle \frac{{4}}{-12}\) < \(\displaystyle \frac{{-3}}{12}\) (vi) \(\displaystyle \frac{{5}}{-11}\) = \(\displaystyle \frac{{-5}}{11}\)
(vii) 0 > \(\displaystyle \frac{{-7}}{6}\) ( 0 is always greater than negative number).
Q9. Which is greater in each of the following:
(i) \(\displaystyle \frac{{2}}{3}\) , \(\displaystyle \frac{{5}}{2}\)
(ii) \(\displaystyle \frac{{-5}}{6}\) , \(\displaystyle \frac{{-4}}{3}\)
(iii) \(\displaystyle \frac{{-3}}{4}\) , \(\displaystyle \frac{{2}}{-3}\)
(iv) \(\displaystyle \frac{{-1}}{4}\) , \(\displaystyle \frac{{1}}{4}\)
(v) -3 \(\displaystyle \frac{{2}}{7}\) , -3 \(\displaystyle \frac{{4}}{5}\)
Solution:
(i) Taking L.C.M to make denominator same
\(\displaystyle \frac{{2×2}}{3×2}\) , \(\displaystyle \frac{{5×3}}{2×3}\)
\(\displaystyle \frac{{4}}{6}\) , \(\displaystyle \frac{{15}}{6}\)
\(\displaystyle \frac{{4}}{6}\) < \(\displaystyle \frac{{15}}{6}\) (ii) Taking L.C.M to make denominator same
\(\displaystyle \frac{{-5×1}}{6×1}\) , \(\displaystyle \frac{{-4×2}}{3×2}\)
\(\displaystyle \frac{{-5}}{6}\) , \(\displaystyle \frac{{-8}}{6}\)
\(\displaystyle \frac{{-5}}{6}\) > \(\displaystyle \frac{{-8}}{6}\)
(iii) Taking L.C.M to make denominator same
\(\displaystyle \frac{{-3×3}}{4×3}\) , \(\displaystyle \frac{{2×4}}{-3×4}\)
\(\displaystyle \frac{{-9}}{12}\) , \(\displaystyle \frac{{8}}{-12}\)
\(\displaystyle \frac{{-9}}{12}\) < [latex]\displaystyle \frac{{8}}{-12}[/latex] (iv) \(\displaystyle \frac{{-1}}{4}\) < \(\displaystyle \frac{{1}}{4}\) (v) converting into improper fraction
-3 \(\displaystyle \frac{{2}}{7}\) = \(\displaystyle \frac{{-23}}{7}\)
-3 \(\displaystyle \frac{{4}}{5}\) = \(\displaystyle \frac{{-19}}{5}\)
Taking L.C.M to make denominator same
\(\displaystyle \frac{{-23×5}}{7×5}\) , \(\displaystyle \frac{{-19×7}}{5×7}\)
\(\displaystyle \frac{{-115}}{35}\) , \(\displaystyle \frac{{-133}}{35}\)
\(\displaystyle \frac{{-115}}{35}\) > \(\displaystyle \frac{{-133}}{35}\)
Q10. Write the following rational numbers in ascending order:
(i) \(\displaystyle \frac{{-3}}{5}\) , \(\displaystyle \frac{{-2}}{5}\) ,\(\displaystyle \frac{{-1}}{5}\)
(ii) \(\displaystyle \frac{{-1}}{3}\) ,\(\displaystyle \frac{{-2}}{9}\) ,\(\displaystyle \frac{{-4}}{3}\)
(iii) \(\displaystyle \frac{{-3}}{7}\) ,\(\displaystyle \frac{{-3}}{2}\) ,\(\displaystyle \frac{{-3}}{4}\)
Solution:
(i) \(\displaystyle \frac{{-3}}{5}\) < \(\displaystyle \frac{{-2}}{5}\) < \(\displaystyle \frac{{-1}}{5}\) (ii) Taking L.C.M to make denominator same
\(\displaystyle \frac{{-1×3}}{3×3}\) ,\(\displaystyle \frac{{-2×1}}{9×1}\) ,\(\displaystyle \frac{{-4×3}}{3×3}\)
\(\displaystyle \frac{{-3}}{9}\) ,\(\displaystyle \frac{{-2}}{9}\) ,\(\displaystyle \frac{{-12}}{9}\)
\(\displaystyle \frac{{-12}}{9}\) < \(\displaystyle \frac{{-3}}{9}\) < \(\displaystyle \frac{{-2}}{9}\) (iii) Taking L.C.M to make denominator same
\(\displaystyle \frac{{-3×4}}{7×4}\) ,\(\displaystyle \frac{{-3×14}}{2×14}\) ,\(\displaystyle \frac{{-3×7}}{4×7}\)
\(\displaystyle \frac{{-12}}{28}\) ,\(\displaystyle \frac{{-42}}{28}\) ,\(\displaystyle \frac{{-21}}{28}\)
\(\displaystyle \frac{{-42}}{28}\) < \(\displaystyle \frac{{-21}}{28}\) < \(\displaystyle \frac{{-12}}{28}\)