NCERT Solutions Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.2

 

Introduction:

Numbers in exponential form obey certain laws, which are :

For any non-zero integers a and b and whole numbers m and n,

a) a^m× aⁿ= a ^{m+ n}

b) a^m ÷ aⁿ =a^m-n

c) (a^m)ⁿ  = a ^{m n}

d) a^m × b^m = (ab)^m

e) a^m ÷ b^m = \(\displaystyle {{(\frac{a}{b})}^{m}}\)

f) a⁰ = 1

g) (-1)^{even number} = 1

h) (-1)^{odd  number} = -1

NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.1

NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.2

NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.3

 

Class 7 Maths Exercise 11.2

(Page-181)

Q1. Using laws of exponents, simplify and write the answer in exponential form:

i) 3²× 3⁴× 3⁸

ii)6¹⁵ ÷ 6¹⁰

iii)a³ × a²

iv) 7^x × 7²

v) (5²)³ ÷ 5³

vi)  2⁵ × 5⁵

vii)  a⁴ × b⁴

viii) ( 3⁴)³

ix) (2²⁰ ÷ 2¹⁵) × 2³

x)  8^t × 8²

Solution: 

i)  3^(2+4+8)

= 3¹⁴

ii)  6^(15-10)

= 6⁵

iii) a⁽³⁺²⁾

= a⁵

iv) 7^(x+2)

v) 5^(2×3) ÷ 5³

= 5⁶ ÷ 5³

= 5^(6-3)

= 5³

vi) ( 2×5)⁵

= 10⁵

vii) (a × b)⁴

viii)  3^(4×3)

= 3¹²

ix)  2^(20-15) × 2³

= 2⁵× 2³

= 2⁽⁵⁺³⁾

= 2⁸

x) 8^(t-2)

 

Q2. Simplify and Express each of the following in exponential form:

i) \(\displaystyle \frac{{{{2}^{3}}\times {{3}^{4}}\times 4}}{{3\times 32}}\)

ii) ((5²)³ ×5⁴)÷ 5⁷

iii) 25⁴  ÷ 5³

iv) \(\displaystyle \frac{{3\times {{7}^{2}}\times {{{11}}^{8}}}}{{21\times {{{11}}^{3}}}}\)

v) \(\displaystyle \frac{{{{3}^{7}}}}{{{{3}^{4}}\times {{3}^{3}}}}\)

vi)  2⁰ + 3⁰+ 4⁰

vii)  2⁰ × 3⁰ ×4⁰

viii) (3⁰ + 2⁰)× 5⁰

ix) \(\displaystyle \frac{{{{2}^{8}}\times {{a}^{5}}}}{{{{4}^{3}}\times {{a}^{3}}}}\)

x) \(\displaystyle (\frac{{{{a}^{5}}}}{{{{a}^{3}}}})\) × a⁸

xi) \(\displaystyle \frac{{{{4}^{5}}\times {{a}^{8}}{{b}^{3}}}}{{{{4}^{5}}\times {{a}^{5}}{{b}^{2}}}}\)

xii) (2³× 2)²

Solution: 

i) \(\displaystyle \frac{{{{2}^{3}}\times {{3}^{4}}\times {{2}^{2}}}}{{3\times {{2}^{5}}}}\)

= \(\displaystyle \frac{{{{2}^{{(3+2)}}}\times {{3}^{4}}}}{{3\times {{2}^{5}}}}\)

= \(\displaystyle \frac{{{{2}^{5}}\times {{3}^{{(4-1)}}}}}{{{{2}^{5}}}}\)

= \(\displaystyle \frac{{{{2}^{5}}\times {{3}^{{(3)}}}}}{{{{2}^{5}}}}\)

= 2^(5-5) × 3³

= 2⁰× 3³

= 1× 3³

= 3³

ii) 5^(2×3)×5⁴)÷ 5⁷

= (5⁶×5⁴)÷ 5⁷

= 5⁽⁶⁺⁴⁾ ÷ 5⁷

= 5¹⁰ ÷ 5⁷

= 5^(10-7)

= 5³

iii) (5²)⁴ ÷5³

= 5^(2×4) ÷5³

= 5⁸ ÷5³

= 5^(8-3)

= 5⁵

iv) \(\displaystyle \frac{{3\times {{7}^{2}}\times {{{11}}^{8}}}}{{3\times 7\times {{{11}}^{3}}}}\)

= \(\displaystyle \frac{{3\times {{7}^{{(2-1)}}}\times {{{11}}^{8}}}}{{3\times {{{11}}^{3}}}}\)

= \(\displaystyle \frac{{3\times {{7}^{{(1)}}}\times {{{11}}^{{(8-3)}}}}}{3}\)

= 7× 11⁵

v) \(\displaystyle \frac{{{{3}^{7}}}}{{{{3}^{{4+3}}}}}\)

= \(\displaystyle \frac{{{{3}^{7}}}}{{{{3}^{7}}}}\)

= 3⁰

= 1

vi) 2⁰ + 3⁰+ 4⁰

= 1+1+1

= 3

vii) 2⁰ × 3⁰ ×4⁰

= 1×1×1

= 1

viii) (3⁰ + 2⁰)× 5⁰

=  (1 + 1)× 1

= (2)× 1

= 2

ix) \(\displaystyle \frac{{{{2}^{8}}\times {{a}^{5}}}}{{{{{({{2}^{2}})}}^{3}}\times {{a}^{3}}}}\)

= \(\displaystyle \frac{{{{2}^{8}}\times {{a}^{5}}}}{{{{2}^{6}}\times {{a}^{3}}}}\)

= \(\displaystyle \frac{{{{2}^{8}}\times {{a}^{{(5-3)}}}}}{{{{2}^{6}}}}\)

= \(\displaystyle \frac{{{{2}^{8}}\times {{a}^{2}}}}{{{{2}^{6}}}}\)

= 2^(8-6) × a²

= 2² × a²

= (2a)²

x) \(\displaystyle ({{a}^{{5-3}}})\times a8\)

= a²× a⁸

= a²⁺⁸

= a¹⁰

xi) \(\displaystyle \frac{{{{4}^{{5-5}}}\times {{a}^{8}}{{b}^{3}}}}{{{{a}^{5}}{{b}^{2}}}}\)

= \(\displaystyle \frac{{{{4}^{0}}\times {{a}^{8}}{{b}^{3}}}}{{{{a}^{5}}{{b}^{2}}}}\)

= \(\displaystyle \frac{{1\times {{a}^{8}}{{b}^{3}}}}{{{{a}^{5}}{{b}^{2}}}}\)

= (a^8-5)(b^3-2)

= a³b¹

= a³b

xii) (2³× 2)²

= (2^3×2)×2²

= 2⁶×2²

= 2⁶⁺²

= 2⁸

 

Q3. Say true or false and justify your answer:

i) 10 × 10¹¹  = 100¹¹

ii) 2³ > 5²

iii) 2³ × 3² = 6⁵

iv) 3⁰ = (1000)⁰

Solution: 

i) False

10¹ × 10¹¹  = 100¹¹

10¹² = (10²)¹¹

10¹²  ≠ 10²²

ii) False

2³ > 5²

2×2×2> 5×5

8<25 iii) False

2³ × 3² = 6⁵

8×9 = 7776

72 ≠ 7776

iv) true

3⁰ = (1000)⁰

1 = 1

Q4. Express each of the following as a product of prime factors only in exponential form:

i) 108 × 192

ii) 270

iii) 729 × 64

iv) 768

Solution:

i) 108 × 192

 

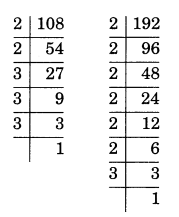
108 × 192 = 2×2×3×3×3×2×2×2×2×2×2×3

= 2⁸ × 3⁴

ii) 

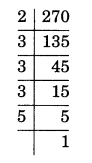
270 = 2×3×3×3×5

= 2 × 3³×5

iii) 

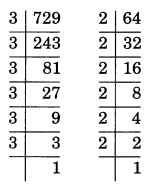
729 × 64= 3×3×3×3×3×3×2×2×2×2×2×2

= 2⁶ × 3⁶

= (2×3)⁶

iv)

768 = 2×2×2×2×2×2×2×2×3

=2⁸ × 3

 

Q5. Simplify:

i) \(\displaystyle \frac{{{{{({{2}^{5}})}}^{2}}\times {{7}^{3}}}}{{{{8}^{3}}\times \,7}}\)

ii) \(\displaystyle \frac{{25\times {{5}^{2}}\times {{t}^{8}}}}{{{{{10}}^{3}}\times {{t}^{4}}}}\)

iii) \(\displaystyle \frac{{{{3}^{5}}\times {{{10}}^{5}}\times 25}}{{{{5}^{7}}\times {{6}^{5}}}}\)

Solution:

i) \(\displaystyle \frac{{{{2}^{{10}}}\times {{7}^{3}}}}{{{{{({{2}^{3}})}}^{3}}\times 7}}\)

= \(\displaystyle \frac{{{{2}^{{10}}}\times {{7}^{3}}}}{{{{2}^{9}}\times 7}}\)

= 2^(10-9) ×7^(3-1)

= 2×7²

= 2×49

=98

ii) \(\displaystyle \frac{{{{5}^{2}}\times {{5}^{2}}\times {{t}^{8}}}}{{{{{(2\times 5)}}^{3}}\times {{t}^{4}}}}\)

= \(\displaystyle \frac{{{{5}^{2}}\times {{5}^{2}}\times {{t}^{{8-4}}}}}{{{{{(2\times 5)}}^{3}}}}\)

= \(\displaystyle \frac{{{{5}^{{(2+2)}}}\times {{t}^{4}}}}{{{{{(2\times 5)}}^{3}}}}\)

= \(\displaystyle \frac{{{{5}^{{(4)}}}\times {{t}^{4}}}}{{{{2}^{3}}\times {{5}^{3}}}}\)

= \(\displaystyle \frac{{{{5}^{{(4-3)}}}\times {{t}^{4}}}}{{{{2}^{3}}}}\)

= \(\displaystyle \frac{{5{{t}^{4}}}}{8}\)

iii) \(\displaystyle \frac{{{{3}^{5}}\times {{{10}}^{5}}\times 25}}{{{{5}^{7}}\times {{6}^{5}}}}\)

= \(\displaystyle \frac{{{{3}^{5}}\times {{{(2\times 5)}}^{5}}\times {{5}^{2}}}}{{{{5}^{7}}\times {{{(2\times 3)}}^{5}}}}\)

= \(\displaystyle \frac{{{{3}^{5}}\times {{2}^{5}}\times {{5}^{5}}\times {{5}^{2}}}}{{{{5}^{7}}\times {{2}^{5}}\times {{3}^{5}}}}\)

= \(\displaystyle \frac{{{{3}^{{5-5}}}\times {{2}^{{5-5}}}\times {{5}^{{5+2}}}}}{{{{5}^{7}}}}\)

= \(\displaystyle \frac{{{{3}^{0}}\times {{2}^{0}}\times {{5}^{7}}}}{{{{5}^{7}}}}\)

= 1×1×5^(7-7)

= 1×7⁰

= 1×1

=1