NCERT Solutions Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.1
Introduction:
In this chapter, Exponents and Power we will learn that very large numbers are difficult to read, understand and compare, we use exponents.
We can write large numbers in a shorter form using Exponents.
For example - 10,000 = 10×10×10×10 = 104
The short notation 104 stands for the product 10×10×10×10. Here, '10' is called the base and '4' the exponent. The number 104 is read as 10 raised to the power of 4 or simply as fourth power of 10. is called the exponential form of 10,000.
NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.1
NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.2
NCERT Class 7 Maths Chapter 11 Exponents and Powers Exercise 11.3
Class 7 Maths Exercise 11.1 (Page-173)
Q1. Find the value of :
(i) \(\displaystyle {{2}^{6}}\)
(ii) 9³
(iii) 11²
(iv) \(\displaystyle {{5}^{4}}\)
Solution:
(i) 2×2×2×2×2×2 = 64
(ii) 9×9×9 = 729
(iii) 11×11 = 121
(iv) 5×5×5×5 = 625
Q2. Exress the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c× c × d
Solution:
(i) \(\displaystyle {{6}^{4}}\)
(ii) \(\displaystyle {{t}^{2}}\)
(iii) \(\displaystyle {{b}^{4}}\)
(iv) \(\displaystyle {{5}^{2}}\) × \(\displaystyle {{7}^{3}}\)
(v) \(\displaystyle {{2}^{2}}\) × \(\displaystyle {{a}^{2}}\)
(vi) \(\displaystyle {{a}^{3}}\) × \(\displaystyle {{c}^{4}}\) × d¹
Q3. Express each of the following numbers using exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Solution: (i)

2 ×2×2×2×2×2×2×2×2 = \(\displaystyle {{2}^{9}}\)
(ii) 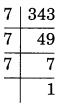
7 × 7× 7 = 7³
(iii) 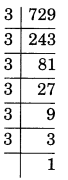
3×3×3×3×3×3 = \(\displaystyle {{3}^{6}}\)
(iv) 
5×5×5×5×5 = \(\displaystyle {{5}^{5}}\)
Q4. Identify the greater number, wherever possible, in each of the following?
(i) 43 or 34
(ii) 53 or 35
(iii) 28 or 82
(iv) 100² or 2100
(v)210 or 102
Solution:
(i) 4³ = 4×4×4 = 64
34= 3×3×3×3= 81
= 64< 81. Hence, 34 is a greater number.
ii) 5³ = 5×5×5 = 125
35 = 3×3×3×3×3 = 243
= 125< 243 Hence, 35 is greater number.
iii) 28 = 2×2×2×2×2×2×2×2 = 256
82 = 8×8 = 64
= 256> 64
Hence, 28 is greater number.
(iv) 100² = 100×100 = 10000
2100= splitting 2100 into 210
210 = 2×2×2×2×2×2×2×2×2×2= 1024
s0, 2100 = 1024×1024×1024×1024×1024×1024×1024×1024×1024×1024
so, 100²<2100
Hence, 2100 is greater number.
(v) 210= 2×2×2×2×2×2×2×2×2×2= 1024
10²= 10×10= 100
1024> 100
hence, 210 is greater number.
Q5. Express each of the following as product of powers of their prime factors:
(i) 648
(ii) 405
(iii) 540
(iv) 3600
Solution:
(i) 648
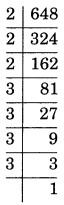
648 = 2×2×2×3×3×3×3
= 2³× \(\displaystyle {{3}^{4}}\)
ii) 405

405 = 3×3×3×3×5
405 = \(\displaystyle {{3}^{4}}\)
iii) 540
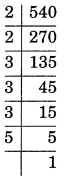
540 = 2×2×3×3×3×5
540= 2² × 3³ × 5
iv) 3600

3600 = 2×2×2×2×3×3×5×5
3600= \(\displaystyle {{2}^{4}}\) × 3² × 5²
Q6. Simplify:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × \(\displaystyle {{4}^{4}}\)
(v) 0 ×10²
(vi) 5² × 3³
(vii) \(\displaystyle {{2}^{4}}\) × 3²
(viii) 3² × \(\displaystyle {{10}^{4}}\)
Solution:
i) 2 × 10× 10× 10= 2× 1000
= 2000
ii) 7×7×2×2
= 49×4
= 196
iii) 2×2×2×5
= 8×5
= 40
iv) 3×4×4×4×4
= 3×16×16
= 48×16
= 768
v) 0( if we multiply any number to zero answer will remain zero)
vi) 5×5×3×3×3
= 25×27
= 675
vii) 2×2×2×2×3×3
= 4×4×9
= 16×9
= 144
viii) 3×3×10×10×10×10
= 9× 10000
= 90000
Q7. Simplify:
(i) (-4)³
(ii) (-3)×(-2)³
(iii) (-3)²× (-5)²
(iv) (-2)³× (-10)³
Solution:
i) -4×-4×-4
= 16 ×-4
= - 64
ii) (-3) × -2 ×-2×-2
= (-3 )×(-8)
= 24
iii) -3×-3×-5×-5
= 9×25
= 225
(iv) -2×-2×-2×-10×-10×-10
= -8)×(-1000)
= 8000
Q8. Compare the following numbers:
(i) 2.7 × 1012 ; 1.5× 108
(ii) 4× 1014; 3× 1017
Solution:
i) 1012 >108
So, 2.7 × 1012 > 1.5× 108
ii) 1014< 1017
So, 4× 1014 <3× 1017