NCERT Solutions Class 11 Maths Chapter 4 COMPLEX NUMBERS AND
QUADRATIC EQUATIONS
Miscellaneous Exercise on Chapter 4
NCERT Solutions Class 11 Maths Chapter 4 Miscellaneous:
Mathematics is a subject that builds the foundation for many advanced concepts, and NCERT textbooks are designed to ensure that students grasp these concepts thoroughly. Chapter 4 in Class 11 Maths, titled "Principle of Mathematical Induction," is a fundamental topic that introduces students to a method of mathematical proof that is both logical and essential for solving complex problems in higher studies.
The Miscellaneous Exercise at the end of this chapter serves as a comprehensive revision tool, integrating various concepts covered throughout the chapter. It challenges students to apply their understanding in different scenarios, ensuring a deeper grasp of the subject matter.
Key Topics Covered in Chapter 4:
- Principle of Mathematical Induction:
Understanding the basic idea of induction, which involves proving a statement for all natural numbers by verifying it for an initial value (usually 1) and then proving that if it holds for an arbitrary positive integer, it must also hold for
.
- Applications of Mathematical Induction:
The chapter illustrates how induction can be applied to prove a variety of statements, including inequalities, divisibility rules, and the sum of sequences.
Benefits of Referring to NCERT Solutions:
- Clarity in Concepts:
The solutions break down complex problems into manageable steps, making it easier for students to understand the logic and approach required to solve them. - Prepared for Exams:
By practicing these solutions, students can be confident in their preparation for exams, as NCERT exercises are often directly referenced in question papers. - Enhances Problem-Solving Skills:
The variety of problems in the Miscellaneous Exercise ensures that students are well-versed in different types of questions, improving their overall problem-solving abilities. - Accessible Learning:
These solutions are freely available online, providing easy access for students to practice and learn at their own pace.
Conclusion
The Miscellaneous Exercise of Chapter 4 in NCERT Class 11 Maths is an essential tool for mastering the principles of mathematical induction. By utilizing the NCERT Solutions, students can ensure they have a strong understanding of the chapter and are well-prepared for their exams. Whether you are looking to clarify doubts or reinforce your learning, these solutions are an invaluable resource in your academic journey.
NCERT Solution Class 11 Maths Chapter 4 Exercise 4.1
NCERT Solution Class 11 Maths Chapter 4 Miscellaneous Exercise
Class 11 Maths Miscellaneous Exercise (Page-85)
Miscellaneous Exercise on Chapter 4








NCERT Solution Class 11 Maths Chapter 4 Exercise 4.1
NCERT Solution Class 11 Maths Chapter 4 Miscellaneous Exercise
Q1. 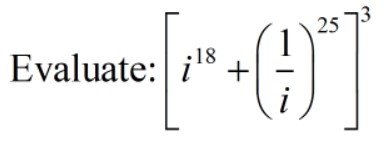
Solution:
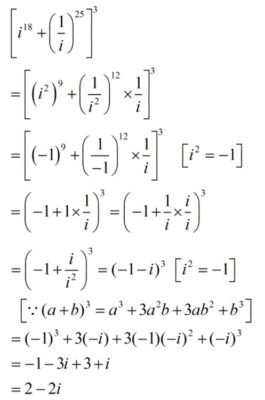
Q2.
![]()
Solution:
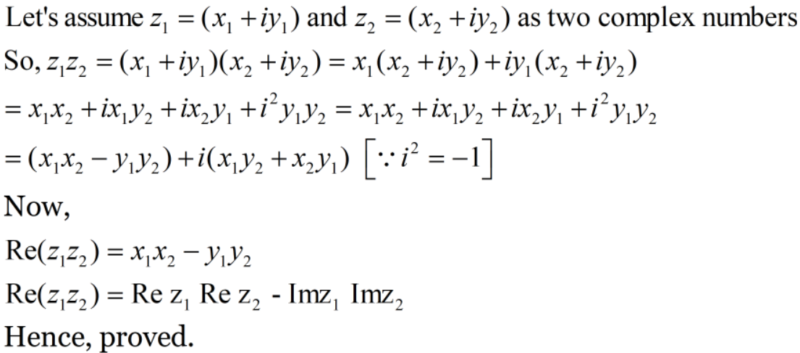

Q3. \(\displaystyle \text{Reduce}\) \(\displaystyle \left( {\frac{1}{{1-4i}}-\frac{2}{{1+i}}} \right)\left( {\frac{{3-4i}}{{5+i}}} \right)\) \(\displaystyle \text{to}\ \text{the}\ \text{standard}\ \text{form}\text{.}\)
Solution:
\(\displaystyle \begin{array}{l}\left( {\frac{1}{{1-4i}}-\frac{2}{{1+i}}} \right)\left( {\frac{{3-4i}}{{5+i}}} \right)\ =\left[ {\frac{{(1+i)-2(1-4i)}}{{(1-4i)(1+i)}}} \right]\left( {\frac{{3-4i}}{{5+i}}} \right)\\=\left[ {\frac{{1+i-2+8i}}{{1+i-4i-4{{i}^{2}}}}} \right]\left( {\frac{{3-4i}}{{5+i}}} \right)\\=\left[ {\frac{{-1+9i}}{{1-3i-4(-1)}}} \right]\left( {\frac{{3-4i}}{{5+i}}} \right)\ \ \ \ \left[∵ {{{i}^{2}}=-1} \right]\end{array}\)
\(\displaystyle \begin{array}{l}=\ \frac{{(-1+9i)(3-4i)}}{{(5-3i)(5+i)}}\ =\frac{{-1(3-4i)+9i(3-4i)}}{{5(5+i)-3i(5+i)}}\\=\ \frac{{-3+4i+27i-36{{i}^{2}}}}{{25+5i-15i-3{{i}^{2}}}}\ \\=\frac{{-3+31i+36}}{{25-10i+3}}\ \ \ \ \ \left[ {{{i}^{2}}=-1} \right]\\=\ \frac{{33+31i}}{{28-10i}}\ =\frac{{33+31i}}{{2(14-5i)}}\\=\frac{{33+31i}}{{2(14-5i)}}\times \frac{{(14+5i)}}{{(14+5i)}}\\=\ \frac{{33(14+5i)+31i(14+5i)}}{{2({{{14}}^{2}}-5{{i}^{2}})}}\ \ \ \ \ \left[∵ {{{i}^{2}}=-1} \right]\\=\ \frac{{462+165i+434i+155{{i}^{2}}}}{{2\{196-25(-1)\}}}\ \\=\ \frac{{462+599i-155}}{{392+50}}\ =\ \frac{{307+599i}}{{442}}\\=\ \frac{{307}}{{442}}+\frac{{599i}}{{442}}\end{array}\)
\(\displaystyle \text{Hence,}\ \text{above}\ \text{is}\ \text{the}\ \text{required}\ \text{standard}\ \text{form}\text{.}\)
Q4. \(\displaystyle \text{If}\ x-iy=\sqrt{{\frac{{a-ib}}{{c-id}}}}\ \text{prove}\ \text{that}\ {{\left( {{{x}^{2}}+{{y}^{2}}} \right)}^{2}}=\frac{{{{a}^{2}}+{{b}^{2}}}}{{{{c}^{2}}+{{d}^{2}}}}\)
Solution:
\(\displaystyle \begin{array}{l}\text{Given}\ x-iy=\sqrt{{\frac{{a-ib}}{{c-id}}}}\ \\\Rightarrow x-iy=\sqrt{{\frac{{a-ib}}{{c-id}}\times \frac{{c+id}}{{c+id}}}}\\\Rightarrow x-iy=\sqrt{{\frac{{(a-ib)(c+id)}}{{{{{(c)}}^{2}}-{{{(id)}}^{2}}}}}}\ \ \ \ \left[ {\text{Squared}\ \text{both}\ \text{sides}} \right]\\\Rightarrow {{(x-iy)}^{2}}=\frac{{(a-ib)(c+id)}}{{{{{(c)}}^{2}}-{{{(id)}}^{2}}}}\\\Rightarrow {{x}^{2}}-i2xy+{{i}^{2}}{{y}^{2}}=\frac{{a(c+id)-ib(c+id)}}{{{{c}^{2}}+{{d}^{2}}}}\ \ \\\Rightarrow {{x}^{2}}-i2xy-{{y}^{2}}=\frac{{ac+iad-ibc+bd}}{{{{c}^{2}}+{{d}^{2}}}}\ \ \ \ \left[ {{{i}^{2}}-1} \right]\\\Rightarrow {{x}^{2}}-{{y}^{2}}-i2xy=\frac{{ac+bd+i(ad-bc)}}{{{{c}^{2}}+{{d}^{2}}}}\ \\\Rightarrow {{x}^{2}}-{{y}^{2}}-i2xy=\frac{{ac+bd}}{{{{c}^{2}}+{{d}^{2}}}}+i\frac{{(ad-bc)}}{{{{c}^{2}}+{{d}^{2}}}}\ \\\text{After}\ \text{comparing}\ \text{real}\ \text{and}\ \text{Imaginary}\ \text{parts,}\ \text{we}\ \text{get}\\{{x}^{2}}-{{y}^{2}}=\frac{{ac+bd}}{{{{c}^{2}}+{{d}^{2}}}},\ and\ -i2xy=i\frac{{(ad-bc)}}{{{{c}^{2}}+{{d}^{2}}}}\ ..........\ (\text{i})\\Now,\ {{({{x}^{2}}+{{y}^{2}})}^{2}}={{({{x}^{2}}-{{y}^{2}})}^{2}}+4{{x}^{2}}{{y}^{2}}\\={{\left( {\frac{{ac+bd}}{{{{c}^{2}}+{{d}^{2}}}}} \right)}^{2}}+{{\left( {\frac{{(ad-bc)}}{{{{c}^{2}}+{{d}^{2}}}}} \right)}^{2}}\ \ \ \ \left[ {\text{by}\ \text{equation}\ \text{(i)}} \right]\end{array}\)
\(\displaystyle \begin{array}{l}=\ \frac{{{{a}^{2}}{{c}^{2}}+{{b}^{2}}{{d}^{2}}+2abcd+{{a}^{2}}{{d}^{2}}+{{b}^{2}}{{c}^{2}}-2abcd}}{{{{{({{c}^{2}}+{{d}^{2}})}}^{2}}}}\\=\ \frac{{{{a}^{2}}{{c}^{2}}+{{a}^{2}}{{d}^{2}}+{{b}^{2}}{{c}^{2}}+{{b}^{2}}{{d}^{2}}}}{{{{{({{c}^{2}}+{{d}^{2}})}}^{2}}}}\\=\ \frac{{{{a}^{2}}({{c}^{2}}+{{d}^{2}})+{{b}^{2}}({{c}^{2}}+{{d}^{2}})}}{{{{{({{c}^{2}}+{{d}^{2}})}}^{2}}}}\ \\=\ \frac{{({{a}^{2}}+{{b}^{2}})({{c}^{2}}+{{d}^{2}})}}{{({{c}^{2}}+{{d}^{2}})({{c}^{2}}+{{d}^{2}})}}\\=\ \frac{{({{a}^{2}}+{{b}^{2}})}}{{({{c}^{2}}+{{d}^{2}})}}\\\text{Hence}\ \text{proved}\text{.}\end{array}\)
Q5. \(\displaystyle \text{If}\ {{z}_{1}}=2-i,\ \ {{z}_{2}}=1+i\ \text{Find}\ {{\left| {\frac{{{{z}_{1}}+{{z}_{2}}+1}}{{{{z}_{1}}-{{z}_{2}}+1}}} \right|}_{.}}\)
Solution:
\(\displaystyle \begin{array}{l}\text{Given,}\\\ {{z}_{1}}=2-i,\ \ {{z}_{2}}=1+i\\\begin{array}{*{20}{c}} \begin{array}{l}\left| {\frac{{{{z}_{1}}+{{z}_{2}}+1}}{{{{z}_{1}}-{{z}_{2}}+1}}} \right|\\=\left| {\frac{{(2-i)+(1+i)+1}}{{(2-i)-(1+i)+1}}} \right|\\=\left| {\frac{4}{{2-2i}}} \right|=\left| {\frac{4}{{2(1-i)}}} \right|.\end{array} \\ {} \\ {=\left| {\frac{2}{{1-i}}\times \frac{{1+i}}{{1+i}}} \right|=\left| {\frac{{2(1+i)}}{{\left( {{{1}^{2}}-{{i}^{2}}} \right)}}} \right|} \\ \begin{array}{l}=\left| {\frac{{2(1+i)}}{{1+1}}} \right|\quad \left[ {{{i}^{2}}=-1} \right]\\=\left| {\frac{{2(1+i)}}{2}} \right|\end{array} \\ {\left[ {∵\left| Z \right|=\sqrt{{{{a}^{2}}+{{b}^{2}}}}} \right]} \end{array}\\\ \ ∴\ | 1+i | =\ \sqrt{{{{1}^{2}}+{{1}^{2}}}}=\sqrt{2}\\So,\ value\ of\ \left| {\frac{{{{z}_{1}}+{{z}_{2}}+1}}{{{{z}_{1}}-{{z}_{2}}+1}}} \right|\ is\ \sqrt{2}\end{array}\)
Q6. If \({a + ib =}\frac{(x + i)^{2}}{2x^{2}{+1}}\) Prove that \(a^{2}+b^{2} = \frac{\left( x^{2}{+1} \right)^{2}}{\left( 2x^{2}{+1} \right)^{2}}\)
Solution:
\(\displaystyle \begin{array}{l}\text{Given}\\(a+ib)=\frac{{{{{(x+i)}}^{2}}}}{{2{{x}^{2}}+1}}\ =\frac{{{{x}^{2}}+{{i}^{2}}+2xi}}{{2{{x}^{2}}+1}}\\=\frac{{{{x}^{2}}-1+i2x}}{{2{{x}^{2}}+1}}\ \ \ \ \left[ {{{i}^{2}}=-1} \right]\\=\frac{{{{x}^{2}}-1}}{{2{{x}^{2}}+1}}+i\left( {\frac{{2x}}{{2{{x}^{2}}+1}}} \right)\\\left[ \begin{array}{l}\text{On}\ \text{comparing}\ \text{Real}\ \text{and}\ \text{Imazinary}\ \text{terms:}\\\text{We}\ \text{get,}\ \ a=\frac{{{{x}^{2}}-1}}{{2{{x}^{2}}+1}},\ b=\frac{{2x}}{{2{{x}^{2}}+1}}\end{array} \right]\\{{a}^{2}}+{{b}^{2}}={{\left( {\frac{{{{x}^{2}}-1}}{{2{{x}^{2}}+1}}} \right)}^{2}}+{{\left( {\frac{{2x}}{{2{{x}^{2}}+1}}} \right)}^{2}}\\=\frac{{{{x}^{4}}+1-2{{x}^{2}}+4{{x}^{2}}}}{{{{{(2x+1)}}^{2}}}}\\=\frac{{{{x}^{4}}+1+2{{x}^{2}}}}{{{{{\left( {2{{x}^{2}}+1} \right)}}^{2}}}}=\frac{{{{{\left( {{{x}^{2}}+1} \right)}}^{2}}}}{{{{{\left( {2{{x}^{2}}+1} \right)}}^{2}}}}\\{{a}^{2}}+{{b}^{2}}=\frac{{{{{\left( {{{x}^{2}}+1} \right)}}^{2}}}}{{{{{\left( {2{{x}^{2}}+1} \right)}}^{2}}}}\\\text{Hence, proved}\end{array}\)
Q7.
\(\displaystyle \begin{array}{l}\text{Let}\ {{z}_{1}}=2-i,\ {{z}_{2}}=-2+i\ \text{Find}\\(\text{i})\ \operatorname{Re}\left( {\frac{{{{z}_{1}}{{z}_{2}}}}{{{{{\bar{z}}}_{1}}}}} \right),\ \ \ \ \ \ \ \ \ (\text{ii})\ \operatorname{Im}\left( {\frac{1}{{{{z}_{1}}{{{\bar{z}}}_{1}}}}} \right)\end{array}\)
Solution:
\(\displaystyle \begin{array}{l}(\text{i})\ \operatorname{Re}\left( {\frac{{{{z}_{1}}{{z}_{2}}}}{{{{{\bar{z}}}_{1}}}}} \right)\\\frac{{{{z}_{1}}{{z}_{2}}}}{{{{{\bar{z}}}_{1}}}}=\frac{{(2-i)(-2+i)}}{{2+i}}\ =\frac{{2(-2+i)-i(-2+i)}}{{2+i}}\\=\frac{{-4+2i+2i-{{i}^{2}}}}{{2+i}}=\frac{{-4+4i+1}}{{2+i}}\ \ \left[ {\because {{i}^{2}}=-1} \right]\\=\frac{{-3+4i}}{{2+i}}\times \frac{{2-i}}{{2-i}}=\frac{{-3(2-i)+4i(2-i)}}{{4-{{i}^{2}}}}\\=\frac{{-6+3i+8i-4{{i}^{2}}}}{{4+1}}\ \ \ \ \left[ {\because {{i}^{2}}=-1} \right]\\=\frac{{-6+11i+4}}{5}=\frac{{-2+11i}}{5}\\=\frac{{-2}}{5}+i\frac{{11}}{5}\\\therefore \operatorname{Re}\left( {\frac{{{{z}_{1}}{{z}_{2}}}}{{{{{\bar{z}}}_{1}}}}} \right)=-\frac{2}{5}\end{array}\)
\(\displaystyle \begin{array}{*{20}{l}} {(\text{ii})\ \operatorname{Im}\left( {\frac{1}{{{{z}_{1}}{{{\bar{z}}}_{1}}}}} \right)} \\ {\frac{1}{{{{z}_{1}}{{{\bar{z}}}_{1}}}}=\frac{1}{{(2-i)(2+i)}}} \\ {=\frac{1}{{{{{(2)}}^{2}}+{{{(i)}}^{2}}}}=\frac{1}{5}\ \ \ \ \ \left[ {\because {{i}^{2}}-1} \right]} \\ {=\frac{1}{5}+i0} \\ {\therefore \operatorname{Im}\left( {\frac{1}{{{{z}_{1}}{{{\bar{z}}}_{1}}}}} \right)=0} \end{array}\)
NCERT Solution Class 11 Maths Chapter 4 Exercise 4.1
NCERT Solution Class 11 Maths Chapter 4 Miscellaneous Exercise