NCERT Solutions Class 11 Maths Chapter 4 COMPLEX NUMBERS AND
QUADRATIC EQUATIONS Exercise 4.1
NCERT Solutions Class 11 Maths Chapter 4: Complex Numbers and Quadratic Equations - Exercise 4.1
Chapter 4 of NCERT Class 11 Maths delves into the topic of Complex Numbers and Quadratic Equations, laying the groundwork for more advanced mathematical concepts. Exercise 4.1 focuses on the basic operations with complex numbers, including addition, subtraction, multiplication, and division. The problems are designed to help students understand the algebraic properties of complex numbers, their geometric representation, and the fundamental principle of conjugates and moduli.
Key Concepts Covered in Exercise 4.1:
- Operations with Complex Numbers: This section involves performing basic arithmetic operations like addition, subtraction, multiplication, and division on complex numbers, helping students get comfortable with handling them.
- Conjugates and Moduli: Understanding the importance of conjugates and moduli in simplifying complex number expressions and solving equations.
- Geometric Representation: Problems that help students visualize complex numbers on the Argand plane, which is crucial for understanding their properties.
- Quadratic Equations: Introduction to solving quadratic equations with complex roots, a key application of complex numbers.
Benefits of NCERT Solutions:
- Detailed Step-by-Step Solutions: Each problem in Exercise 4.1 is broken down into detailed steps, ensuring students can follow the logic and methodology used to arrive at the correct answer.
- Conceptual Clarity: The solutions provide explanations for each step, reinforcing the underlying concepts and helping students grasp the material more effectively.
- Preparation for Exams: Regular practice with these solutions ensures that students are well-prepared for their exams, as they cover all possible types of questions that can be asked from this chapter.
- Improved Problem-Solving Skills: By working through these problems, students enhance their problem-solving abilities, which are crucial for tackling more complex mathematical challenges in future studies.
Conclusion
In conclusion, the NCERT Solutions for Class 11 Maths Chapter 4 Exercise 4.1 are an invaluable resource for mastering the basics of complex numbers and quadratic equations. With these solutions, students can build a strong foundation, ensuring they are well-prepared for both their exams and higher-level mathematics courses.
NCERT Solution Class 11 Maths Chapter 4 Exercise 4.1
NCERT Solution Class 11 Maths Chapter 4 Miscellaneous Exercise
Class 11 Maths Exercise 4.1 (Page-82)
EXERCISE 4.1





Express each of the complex number given in the Exercises 1 to 10 in the
form a + ib.
Q1. 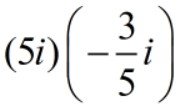
Solution:
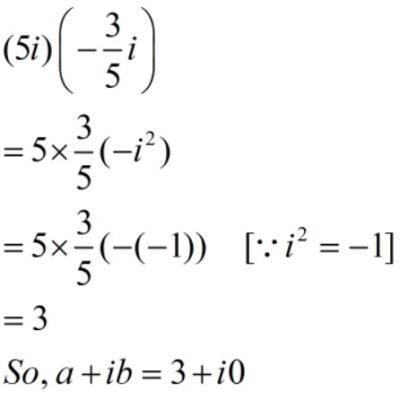
Q2. \(\displaystyle {{i}^{9}}+{{i}^{{19}}}\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {{{i}^{9}}+{{i}^{{19}}}} \\ {={{i}^{{2\times 4+1}}}+{{i}^{{2\times 9+1}}}} \\ {={{{({{i}^{2}})}}^{4}}\times i+{{{({{i}^{2}})}}^{9}}\times i} \\ {={{{(-1)}}^{4}}\times i+{{{(-1)}}^{9}}\times i\ \ \ \ \ [∵{{i}^{2}}=-1]} \\ {=1\times i+(-1)\times i} \\ {=i-i} \\ {=0} \\ {So,\ a+ib=0+i0} \end{array}\)
Q3. \(\displaystyle {{i}^{{-39}}}\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {{{i}^{{-39}}}} \\ {=\frac{1}{{{{i}^{{39}}}}}=\frac{1}{{{{i}^{{2\times 19+1}}}}}} \\ {=\frac{1}{{{{{({{i}^{2}})}}^{{19}}}\times i}}=\frac{1}{{{{{({{i}^{2}})}}^{{19}}}\times i}}\ \ \ \ \ } \\ {=\frac{1}{{{{{(-1)}}^{{19}}}\times i}}\ \ \ \ \ [∵{{i}^{2}}=-1]} \\ {=\frac{1}{{(-1)\times i}}\ =\frac{1}{{(-1)\times i}}\ \times \frac{i}{i}} \\ {=\frac{i}{{(-1)\times {{i}^{2}}}}=\frac{i}{{(-1)\times (-1)}}} \\ {=\frac{i}{1}=i} \\ {So,\ a+ib=0+i1} \end{array}\)
Q4. \(\displaystyle 3(7+i7)+i(7+i7)\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {3(7+i7)+i(7+i7)} \\ {=21+i21+i7+{{i}^{2}}7\ \ } \\ {=21+i28-7\ \ \ \ \ \ \ \ \ [∵{{i}^{2}}=-1]} \\ {\begin{array}{*{20}{l}} {=14+i28} \\ {So,\ a+ib=14+28i} \end{array}} \end{array}\)
Q5. \(\displaystyle (1-i)-(-1+i6)\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {(1-i)-(-1+i6)} \\ {=1-i+1-i6\ } \\ {So,\ a+ib=2-i7} \end{array}\)
Q6. \(\displaystyle \left( {\frac{1}{5}+i\frac{2}{5}} \right)-\left( {4+i\frac{5}{2}} \right)\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {\left( {\frac{1}{5}+i\frac{2}{5}} \right)-\left( {4+i\frac{5}{2}} \right)} \\ {=\frac{1}{5}+i\frac{2}{5}-4-i\frac{5}{2}} \\ {=\frac{1}{5}-4+i\frac{2}{5}-i\frac{5}{2}\ \ \ } \\ {=\frac{{1-20}}{5}+i\left( {\frac{2}{5}-\frac{5}{2}} \right)} \\ {=\frac{{-19}}{5}+i\left( {\frac{{2\times 2}}{{5\times 2}}-\frac{{5\times 5}}{{2\times 5}}} \right)} \\ {=\frac{{-19}}{5}+i\left( {\frac{4}{{10}}-\frac{{25}}{{10}}} \right)} \\ {=\frac{{-19}}{5}+i\left( {\frac{{4-25}}{{10}}} \right)} \\ {=\frac{{-19}}{5}+i\left( {\frac{{-21}}{{10}}} \right)} \\ {So,\ a+ib=\frac{{-19}}{5}-\frac{{21i}}{{10}}} \end{array}\)
Q7. \(\displaystyle \left[ {\left( {\frac{1}{3}+i\frac{7}{3}} \right)+\left( {4+i\frac{1}{3}} \right)} \right]-\left( {-\frac{4}{3}+i} \right)\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {\left[ {\left( {\frac{1}{3}+i\frac{7}{3}} \right)+\left( {4+i\frac{1}{3}} \right)} \right]-\left( {-\frac{4}{3}+i} \right)} \\ {=\left[ {\left( {\frac{1}{3}+4} \right)+i\left( {\frac{7}{3}+\frac{1}{3}} \right)} \right]+\frac{4}{3}-i} \\ {=\frac{{1+12}}{3}+i\left( {\frac{{7+1}}{3}} \right)+\frac{4}{3}-i\ \ } \\ {=\frac{{13}}{3}+\frac{4}{3}+i\left( {\frac{8}{3}-1} \right)} \\ {=\frac{{13+4}}{3}+i\left( {\frac{{8-3}}{3}} \right)} \\ {So,\ a+ib=\frac{{17}}{3}+i\frac{5}{3}} \end{array}\)
Q8. \(\displaystyle {{(1-i)}^{4}}\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {{{{(1-i)}}^{4}}} \\ {={{{\left[ {{{{(1-i)}}^{2}}} \right]}}^{2}}} \\ {={{{\left[ {(1-2i+{{i}^{2}})} \right]}}^{2}}} \\ {={{{\left[ {(1-2i-1)} \right]}}^{2}}} \\ {={{{\left[ {(-2i)} \right]}}^{2}}={{{(-2i)}}^{2}}} \\ {=4{{i}^{2}}} \\ {=4(-1)\ \ \ [∵{{i}^{2}}=-1]} \\ {=-4} \\ {So,\ a+ib=-4+i0} \end{array}\)
Q9. \(\displaystyle {{\left( {\frac{1}{3}+3i} \right)}^{3}}\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} {We\ know\ {{{(a+b)}}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}} \\ {here\ a=\frac{1}{3}\ and\ b=3i} \end{array}} \right]} \\ {So,\ {{{\left( {\frac{1}{3}+3i} \right)}}^{3}}} \\ {={{{\left( {\frac{1}{3}} \right)}}^{3}}+3{{{\left( {\frac{1}{3}} \right)}}^{2}}\times 3i+3\left( {\frac{1}{3}} \right)\times {{{(3i)}}^{2}}+{{{(3i)}}^{3}}} \\ {=\frac{1}{{27}}+3\times \frac{1}{{3\times 3}}3i+3\times \frac{1}{3}\times 9{{i}^{2}}+27{{i}^{3}}} \\ {=\frac{1}{{27}}+i+9{{i}^{2}}+27{{i}^{3}}} \\ {=\frac{1}{{27}}+i+9(-1)+27(-1)i\ \ \ \ [∵{{i}^{2}}=-1]} \\ {=\frac{1}{{27}}+i-9-27i} \\ {=\frac{1}{{27}}-9-26i} \\ {=\frac{{1-27\times 9}}{{27}}-26i} \\ {=\frac{{1-243}}{{27}}-26i} \\ {So,\ a+ib=\frac{{-242}}{{27}}-26i} \end{array}\)
Q10. \(\displaystyle {{\left( {-2-\frac{1}{3}i} \right)}^{3}}\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} {We\ know\ {{{(a+b)}}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}} \\ {here\ a=2\ and\ b=\frac{1}{3}i} \end{array}} \right]} \\ {So,\ {{{\left( {-2-\frac{1}{3}i} \right)}}^{3}}} \\ {=-{{{\left( {2+\frac{1}{3}i} \right)}}^{3}}} \\ {=-\left[ {{{{\left( 2 \right)}}^{3}}+3{{{\left( 2 \right)}}^{2}}\times \frac{1}{3}i+3\left( 2 \right)\times {{{\left( {\frac{1}{3}i} \right)}}^{2}}+{{{\left( {\frac{1}{3}i} \right)}}^{3}}} \right]} \\ {=-\left[ {8+4i+\frac{2}{3}{{i}^{2}}+\frac{{{{i}^{2}}\times i}}{{{{3}^{3}}}}} \right]} \\ {=-\left[ {8+4i-\frac{2}{3}-\frac{i}{{27}}} \right]\ \ \ \ \ [∵{{i}^{2}}=-1]} \\ {=-\left[ {8-\frac{2}{3}+4i-\frac{i}{{27}}} \right]\ \ } \\ {=-\left[ {\frac{{24-2}}{3}+\frac{{(108-1)i}}{{27}}} \right]\ \ } \\ {=-\left[ {\frac{{22}}{3}+\frac{{107i}}{{27}}} \right]\ \ } \\ {So,\ a+ib=-\frac{{22}}{3}-i\frac{{107}}{{27}}\ } \end{array}\)
Find the multiplicative inverse of each of the complex numbers given in the
Exercises 11 to 13.
Q11. \(\displaystyle 4-3i\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {Let,\ Z=4-3i} \\ {So,\ \ \bar{Z}=4+3i} \\ {\left| Z \right|=\sqrt{{{{a}^{2}}+{{b}^{2}}}}\ \ \ \ } \\ {=\sqrt{{{{4}^{2}}+{{3}^{2}}}}\ \ \ \ \left[ {\begin{array}{*{20}{l}} {Given\ 4-3i} \\ {So,\ \ a=4,\ b=3} \end{array}} \right]} \\ {=\sqrt{{16+9}}\ } \\ {=\sqrt{{25}}\ \ =5} \\ {TheMultiplicative\text{ }inverse\text{ }of4-3i} \\ {{{Z}^{{-1}}}=\frac{{\bar{Z}}}{{{{{\left| Z \right|}}^{2}}}}=\frac{{4+3i}}{{{{{(5)}}^{2}}}}=\frac{{4+3i}}{{25}}} \\ {=\frac{4}{{25}}+i\frac{3}{{25}}} \end{array}\)
Q12. \(\displaystyle \sqrt{5}+3i\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {Let,\ Z=\sqrt{5}+3i} \\ {So,\ \ \bar{Z}=\sqrt{5}-3i} \\ {\left| Z \right|=\sqrt{{{{a}^{2}}+{{b}^{2}}}}\ \ \ \ } \\ {=\sqrt{{{{{\left( {\sqrt{5}} \right)}}^{2}}+{{3}^{2}}}}\ \ \ \ \left[ {\begin{array}{*{20}{l}} {Given\ \sqrt{5}+3i} \\ {∴\ a=\sqrt{5},\ b=3} \end{array}} \right]} \\ {=\sqrt{{5+9}}\ } \\ {=\sqrt{{14}}\ \ } \\ {TheMultiplicative\text{ }inverse\text{ }of\sqrt{5}+3i} \\ {{{Z}^{{-1}}}=\frac{{\bar{Z}}}{{{{{\left| Z \right|}}^{2}}}}=\frac{{\sqrt{5}-3i}}{{{{{\left( {\sqrt{{14}}} \right)}}^{2}}}}=\frac{{\sqrt{5}-3i}}{{14}}} \\ {=\frac{{\sqrt{5}}}{{14}}-i\frac{3}{{14}}} \end{array}\)
Q13. \(\displaystyle -i\)
Solution:
\(\displaystyle \begin{array}{*{20}{l}} {Let,\ Z=-i=0-i} \\ {So,\ \ \bar{Z}=0+i=i} \\ {\left| Z \right|=\sqrt{{{{a}^{2}}+{{b}^{2}}}}\ \ \ \ } \\ {\ \ \ \ =\sqrt{{{{{\left( 0 \right)}}^{2}}+{{1}^{2}}}}\ \ \ \ \left[ {\begin{array}{*{20}{l}} {Given\ 0-i} \\ {So,\ a=0,\ b=1} \end{array}} \right]} \\ {\ \ \ \ =\sqrt{{{{1}^{2}}}}\ =1\ } \\ {TheMultiplicative\text{ }inverse\text{ }of\ -i\ } \\ {{{Z}^{{-1}}}=\frac{{\bar{Z}}}{{{{{\left| Z \right|}}^{2}}}}=\frac{i}{{{{{\left( 1 \right)}}^{2}}}}} \\ {\ \ \ \ \ =\frac{i}{1}=i=0+i1} \end{array}\)
Q14. Express the following expression in the form of a+ib :
\(\displaystyle \frac{{\left( {3+i\sqrt{5}} \right)\left( {3-i\sqrt{5}} \right)}}{{\left( {\sqrt{3}+\sqrt{2}i} \right)\left( {\sqrt{3}-i\sqrt{2}} \right)}}\)
Solution:
\(\displaystyle \begin{array}{l}\frac{{\left( {3+i\sqrt{5}} \right)\left( {3-i\sqrt{5}} \right)}}{{\left( {\sqrt{3}+\sqrt{2}i} \right)\left( {\sqrt{3}-i\sqrt{2}} \right)}}\\=\frac{{{{{\left( 3 \right)}}^{2}}-{{{\left( {i\sqrt{5}} \right)}}^{2}}}}{{\left( {\sqrt{3}+\sqrt{2}i} \right)-\left( {\sqrt{3}-i\sqrt{2}} \right)}}\ \ \\\left[ \begin{array}{l}{{a}^{2}}-{{b}^{2}}=(a+b)(a-2)\\here\ a=3,\ b=i\sqrt{5}\end{array} \right]\\=\frac{{9-\left( {{{i}^{2}}5} \right)}}{{\sqrt{3}+\sqrt{2}i-\sqrt{3}+i\sqrt{2}}}\ \\=\frac{{9-\left( {-5} \right)}}{{\sqrt{2}i+i\sqrt{2}}}\ \ \ \ \ \ \ \ \ \left[ {{{i}^{2}}=-1} \right]\\=\frac{{9+5}}{{i2\sqrt{2}}}\ \\=\frac{{14}}{{i2\sqrt{2}}}\times \frac{{i\sqrt{2}}}{{i\sqrt{2}}}\ =\frac{{i7\sqrt{2}}}{{{{i}^{2}}\times 2}}\\=-i\frac{{7\sqrt{2}}}{2}\\So,\ a+ib=0-i\frac{{7\sqrt{2}}}{2}\end{array}\)